学法导航
1. 已知函数y=Asin(ωx+φ)(A>0,ω>0)的图象求解析式时,常采用待定系数法,由图中的最高点、最低点或特殊点求A;由函数的周期确定ω;确定φ常根据“五点法”中的五个点求解,其中一般把第一个零点作为突破口,可以从图象的升降找准第一个零点的位置.
2. 在图象变换过程中务必分清是先相位变换,还是先周期变换.变换只是相对于其中的自变量x而言的,如果x的系数不是1,就要把这个系数提取后再确定变换的单位长度和方向.

3. 函数y=Asin(ωx+φ)的性质及应用的求解思路:第一步:先借助三角恒等变换及相应三角函数公式把待求函数化成y=Asin(ωx+φ)+B的形式;第二步:把“ωx+φ”视为一个整体,借助复合函数性质求y=Asin(ωx+φ)+B的单调性及奇偶性、最值、对称性等问题.
4. (1)三角变换的关键在于对两角和与差的正弦、余弦、正切公式,二倍角公式,三角恒等变换公式的熟记和灵活应用,要善于观察各个角之间的联系,发现题目所给条件与恒等变换公式的联系,公式的使用过程要注意正确性,要特别注意公式中的符号和函数名的变换,防止出现“张冠李戴”的情况.(2)求角问题要注意角的范围,要根据已知条件将所求角的范围尽量缩小,避免产生增解.
5.关于解三角形问题,一般要用到三角形的内角和定理,正弦、余弦定理及有关三角形的性质,常见的三角变换方法和原则都适用,同时要注意“三统一”,即“统一角、统一函数、统一结构”,这是使问题获得解决的突破口.
【高频考点突破】
考点1 三角函数的定义、同角三角函数基本关系式、诱导公式的应用
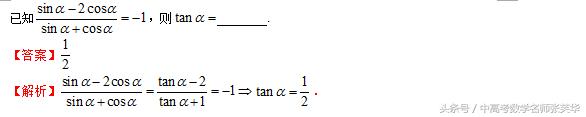
【规律方法】
1、利用三角函数定义将角的终边上点的坐标和三角函数值建立了联系,但是注意角的顶点在坐标原点,始边在x轴的非负半轴.
2.温馨提示:(1)求同角三角函数有知一求三规律,可以利用公式求解,最好的方法是利用画直角三角形速解.(2)利用平方关系求三角函数值时,注意开方时要结合角的范围正确取舍“± ”号.
3. 利用诱导公式化简、证明
i.利用诱导公式化简三角函数的原则和要求
(1)原则:遵循诱导公式先行的原则,即先用诱导公式化简变形,达到角的统一,再进行三角函数名称转化,以保证三角函数名称最少.
(2)要求:①化简过程是恒等变形;②结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值.
ii.证明三角恒等式的主要思路
(1)由繁到简法:由较繁的一边向简单一边化简.
(2)左右归一法:使两端化异为同,把左右式都化为第三个式子.
(3)转化化归法:先将要证明的结论恒等变形,再证明.

考点2 三角函数的图像与性质

考点3 三角恒等变换
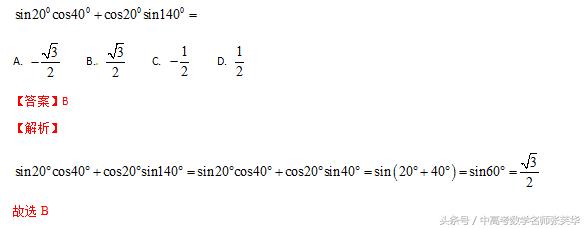
【规律方法】
.三角函数的化简、计算、证明的恒等变形的基本思路与基本的技巧
基本思路是:一角二名三结构.即首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心.第二看函数名称之间的关系,通常“切化弦”;第三观察代数式的结构特点.
考点4解三角形

【规律方法】1.在解三角形时,三角形内角的正弦值一定为正,但该角不一定是锐角,也可能为钝角(或直角),这往往造成有两解,应注意分类讨论,但三角形内角的余弦值为正,该角一定为锐角,且有唯一解,因此,在解三角形中,若有求角问题,应尽量求余弦值.
2.关于解三角形问题,一般要用到三角形的内角和定理,正、余弦定理及有关三角形的性质,常见的三角变换方法和原则都适用,同时要注意“三统一”,即“统一角、统一函数、统一结构”,这是使问题获得解决的突破口.
考点5 解三角形在实际生活中应用
【规律方法】三角形应用题的解题要点:解斜三角形的问题,通常都要根据题意,从实际问题中寻找出一个或几个三角形,然后通过解这些三角形得出所要求的量,从而得到实际问题的解.有些时候也必须注意到三角形的特殊性,如直角三角形、等腰三角形、锐角三角形等.正确理解和掌握方位角、俯角、仰角对于解决三角形应用题也是必不可少的.
把握解三角形应用题的四步:
(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系;
(2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型;
(3)根据题意选择正弦定理或余弦定理求解;
(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.
求距离问题的注意事项:
(1)选定或确定要求解的三角形,即所求量所在的三角形,若其他量已知则直接解;若有未知量,则把未知量放在另一确定三角形中求解.
(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.
求解高度问题应注意:
(1)在测量高度时,要理解仰角、俯角的概念,仰角和俯角都是在同一铅垂面内,视线与水平线的夹角;
(2)准确理解题意,分清已知条件与所求,画出示意图;
(3)运用正、余弦定理,有序地解相关的三角形,逐步求解问题的答案,注意方程思想的运用.
解决测量角度问题的注意事项:
(1)明确方位角的含义;
(2)分析题意,分清已知与所求,再根据题意正确画出示意图,这是最关键、最重要的一步;
(3)将实际问题转化为可用数学方法解决的问题后,注意正、余弦定理的“联袂”使用.
 加载中,请稍侯......
加载中,请稍侯......
精彩评论