高考数学压轴题突破140 破解平面解析几何三大热点题型

热点一 直线与圆

【考向预测】直线方程是解析几何的基础,高考中主要考查基本概念和求在不同条件下的直线方程;两条直线平行与垂直的判定;两条直线的交点和距离问题等, 有时与其它知识（如充要条件、导数的几何意义等）相结合，考查直线与方程的应用.一般以选择题、填空题的形式考查.对于圆的考查,主要是结合直线的方程用几何法或待定系数法确定圆的标准方程及一般方程;利用圆的性质求动点的轨迹方程;直线与圆,圆与圆的位置关系等问题,其中含参数问题为命题热点.浙江省直线与圆问题一般以直线与圆位置关系为主,难度不大,题型主要是选择题或者填空题;解答题中也有考查直线与圆问题,并且更多的是综合在圆锥曲线中进行,难度较大.

热点二 椭圆、双曲线、抛物线的几何性质

【考向预测】圆锥曲线是高考的重点和热点,是高考中每年必考的内容.主要考查圆锥曲线的标准方程、几何性质、直线与圆锥曲线的位置关系等内容.对圆锥曲线方程与性质的考查,以选择题、填空题为主,主要考查求曲线的方程和研究曲线的离心率及双曲线的渐近线等性质.直线与圆锥曲线的位置关系等综合问题依然以直线与抛物线（或椭圆）问题为主，难度较大.

热点三 圆锥曲线的热点问题

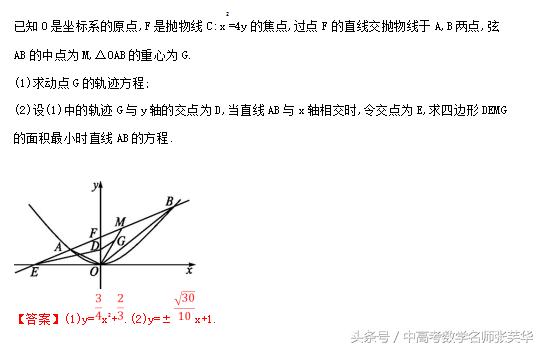
【考向预测】(1)圆锥曲线的综合问题，一般以直线与椭圆或抛物线的位置关系为背景,考查弦长、定点、定值、最值、范围问题或探索性问题,试题难度较大.

(2)求轨迹方程也是高考的热点与重点,若在客观题中出现通常用定义法,若在解答题中出现一般用直接法、代入法、参数法或待定系数法,往往出现在解答题的第(1)问中.

点睛：

求解直线和曲线过定点问题的基本思路是把直线或曲线方程中的变量x,y当作常数看待,并把方程一端化为零,既然是过定点,那么这个方程要对任意参数都成立,这时参数的系数就要全部等于零,这样就得到一个关于x,y的方程组,这个方程组的解所确定的点就是直线或曲线所过的定点.

1.存在性问题,先假设存在,推证满足条件的结论,若结论正确则存在,若结论不正确则不存在.注意以下几点:

(1)当条件和结论不唯一时要分类讨论.

(2)当给出结论而要推导出存在的条件时,先假设成立,再推出条件.

(3)当条件和结论都不知,按常规方法解题很难时,要思维开放,采取另外的途径.

2.存在性问题的解题步骤:

(1)先假设存在,引入参变量,根据题目条件列出关于参变量的方程(组)或不等式(组).

(2)解此方程(组)或不等式(组),若有解则存在;若无解则不存在.

(3)得出结论.