几何光学是高考的必考内容,年年都有考题,涉及的知识点有光的折射定律、折射率、全反射、光导纤维等,主要考查考生作光路图、综合运用光学知识和几何知识处理问题的能力。本文以常见的玻璃砖为例,探讨这类问题的解题方法。
平行玻璃砖
平行玻璃砖对光线的控制作用(如图l所示)是使光线平行移动,即出射光线与入射光线的传播方向相同,出射光线相对入射光线而言只是向“入射光线倾斜方向”发生了侧移。



对于几何光学方面的试题,应用光路图或有关几何图形进行分析与公式配合,将一个物理问题转化为一个几何问题,能够做到直观、形象,易于发现隐舍条件,有利于启迪思维,理顺思路。
三棱镜
三角形玻璃砖即为三棱镜。光线射到三棱镜后,射出的光线偏向三棱镜底边.我们把出射光线与入射光线间的夹角θ叫作偏向角。偏向角的大小与棱镜的材料、棱镜的形状及入射角的大小有关。棱镜材料相对周围介质的折射率越大,偏向角越大。通过三棱镜,在物体的另一 侧看到的是物体的虚像,且相对物而言,像向顶角方向偏移。三棱镜可以用来观察白光的色散现象。


画好典型光路是解决几何光学的基础.光线射到不同面时反射和折射情况会不同,要注意分区域讨论,防止漏解。要细致地分析光线从玻璃砖内部到达每一个界面时的反射和折射情况,尤其要判断是否会发生全反射。
半圆柱形玻璃砖
截面是圆形的玻璃砖,光路对于中轴线有较好的旋转对称性,且当入射光射到圆弧面上时,其入射点到中轴线的垂线就是法线。

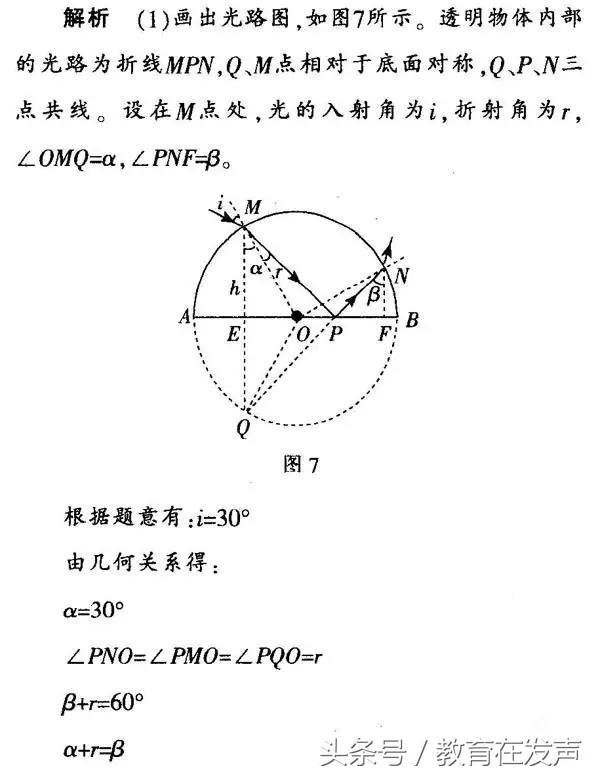
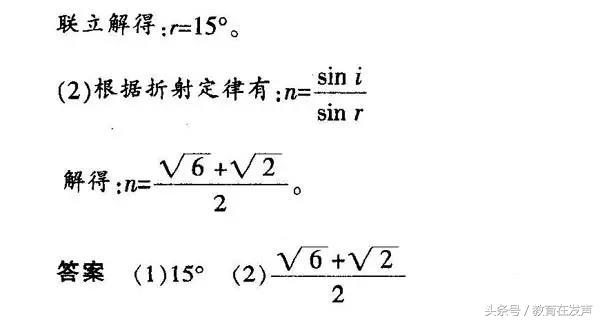
本题以半圆柱形透明物体为载俸,将光的折射和光的反射综合进行考查。解决这类问题的基本思路是:依据题意正确画出光路图,利用几何关系找出入射角和折射角,应用折射定律求解。
圆柱形玻璃砖
圆柱形玻璃砖的截面是圆形。当光线垂直于中轴线射入圆柱形玻璃砖内部时,光路具有很好的对称性。
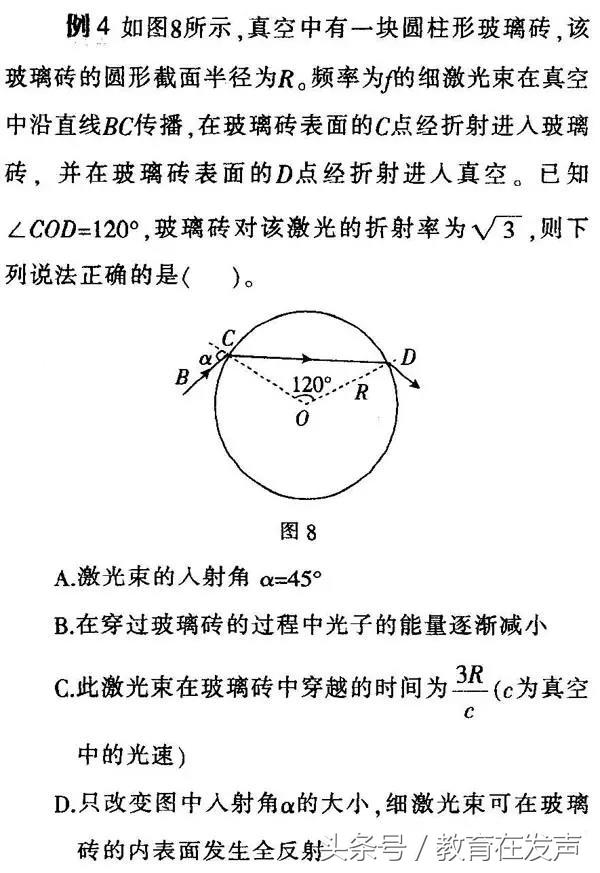


本题考查几何光学、光的折射等知识,在处理几何光学问题时一定要画出光路图.通过图中的几何关系结合几何光学的基本原理得出结论。
玻璃球
玻璃球的截面也是圆形,因此在球形玻璃砖内部,其光路的几何构建与圆柱形玻璃砖内的光路几何构建有相同之处。
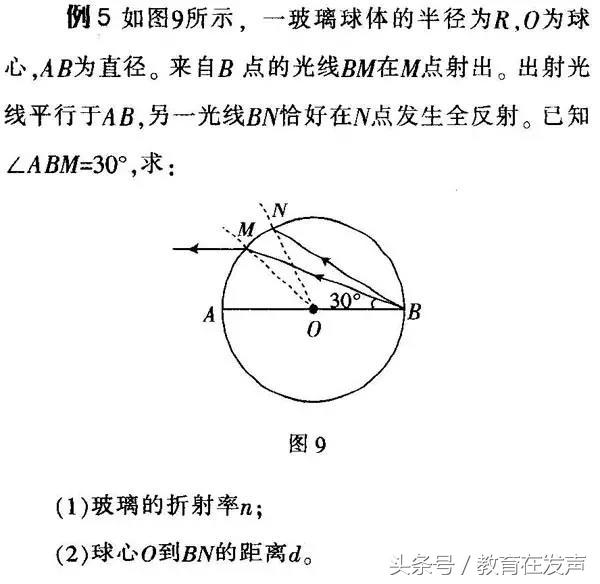

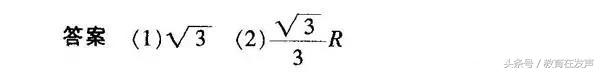
本题考查光的折射和全反射,依据光路图中的几何关系,结合几何光学的基本原理得出各物理量的关系,是解题的基本思路。
组合型玻璃砖
有些玻璃砖的截面是多种几何图形(三角形、扇形等)的组合,这些玻璃砖我们可称为组合型玻璃砖.
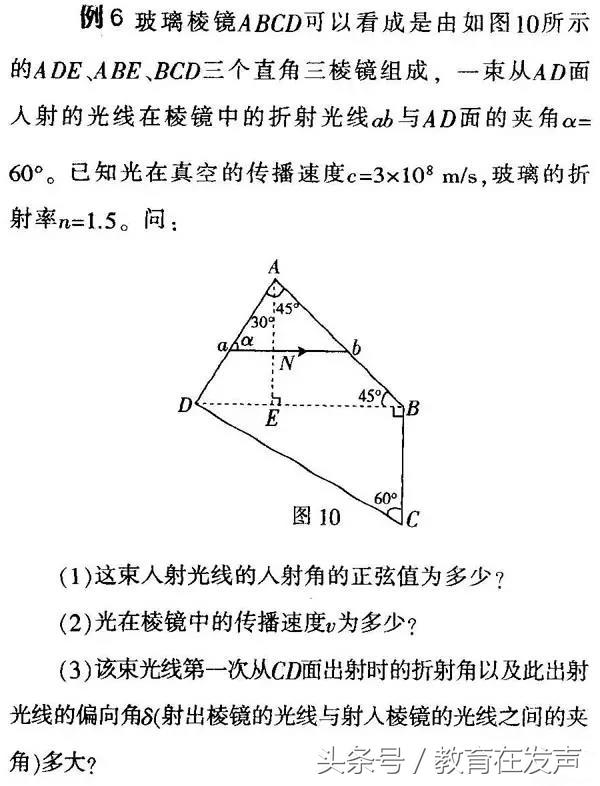

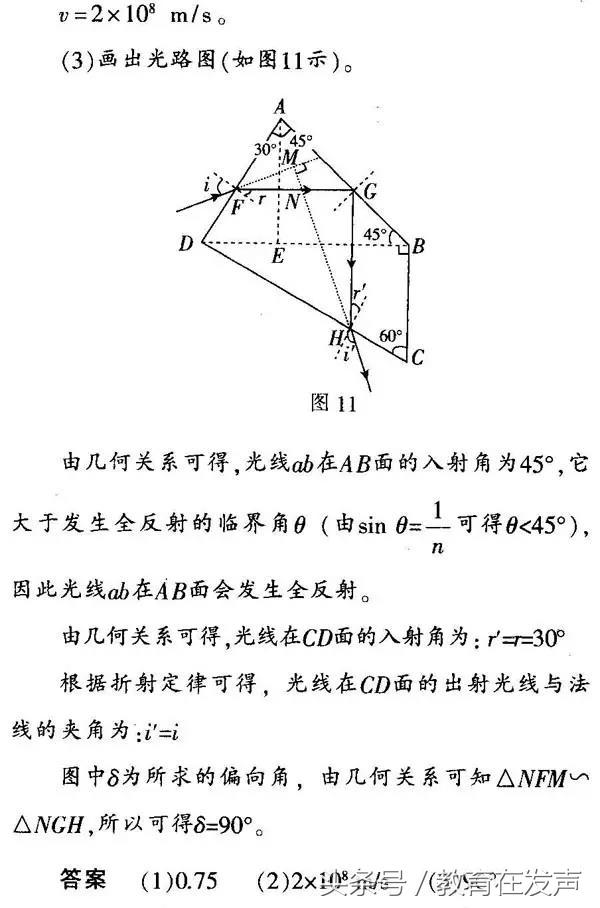
在分析几何光学问题时,一定要作好光路图,依据几何关系求出入射角和折射角;同时注意是否会发生全反射。
除了上面列举的几种玻璃砖外,常见的玻璃砖还有扇形玻璃砖膏空心球形玻璃砖等甜不管是以哪种玻璃砖为载体,虽然形状各异,但是处理方法却相同,即首先画好光路图,特别是典型光路及临界光路,再依据几何关系和物理规律列式解答.
 加载中,请稍侯......
加载中,请稍侯......
精彩评论