反比例函数与几何综合的处理思路

1. 从关键点入手．通过关键点坐标和横平竖直线段长的互相转化，可将函数特征与几何特征综合在一起进行研究．

2. 对函数特征和几何特征进行转化、组合，列方程求解．若借助反比例函数模型，能快速将函数特征转化为几何特征．

与反比例函数相关的几个模型，在解题时可以考虑调用．

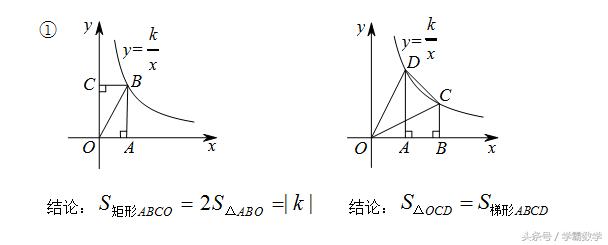
反比例与面积问题

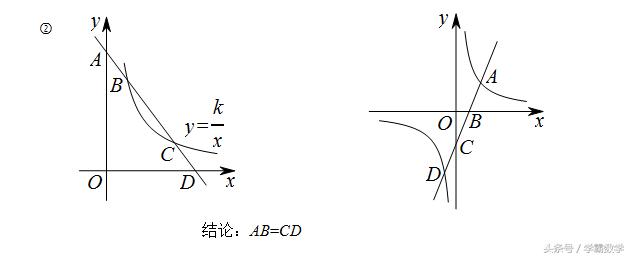
线段等量关系

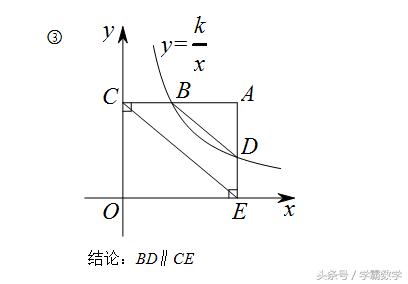
平行关系

证明１

由反比例函数的几何性质有SΔOAD=SΔOCB

SΔOCD=SOBCD-SΔOBC=SOBCD-SOAD=S梯形ABCD

证明２

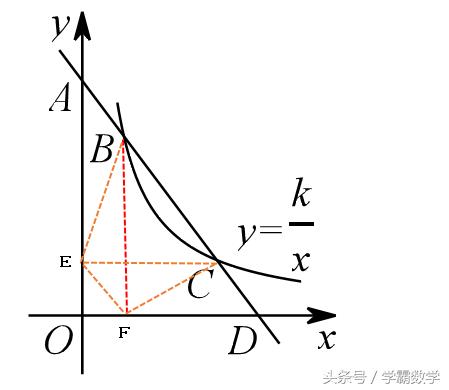
辅助线是关键

分别过Ｂ、Ｃ两点，作x、y轴垂线，连接ＢＥ和ＣＦ

因为ＢＦ平行于Ｙ轴，所以ＳΔＢＥＦ＝ＳΔＢＦＯ（同底等高）

同理ＣＥ平行于Ｘ轴，所以ＳΔＥＦＣ＝ＳΔＥＣＯ（同底等高）

故ＳΔＥＦＢ＝ＳΔＥＦＣ　　得到　　ＥＦ平行于ＡＤ

四边形ＡＢＦＥ和ＣＤＦＥ都为平行四边形（两组对边平行）

所以ＡＢ＝ＣＤ

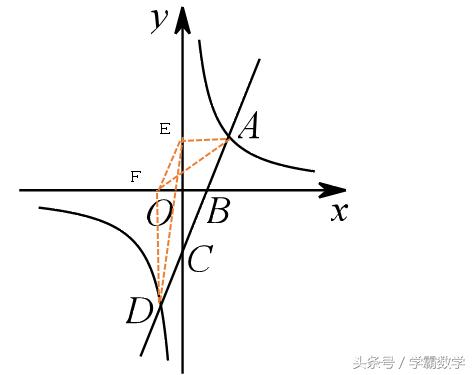
一样的证明思路

过A、D分别作ＸＹ轴的垂线，连接ＡＦ、ＤＥ

SΔDFE=SΔDFO SΔAFE=SΔAEO (同底等高）

所以ＳΔＥＦＡ＝ＳΔＥＦＤ　所以得到ＥＦ平行于ＡＤ

四边形ＥＦＢＡ和ＥＦＤＣ都是平行四边形

所以ＡＢ＝ＣＤ

证明３

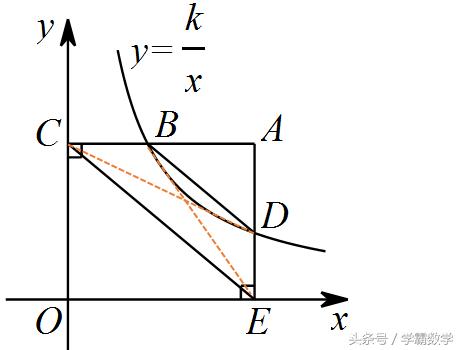
同理可得

同样运用同底等高可以证明，相信你也可以的！

以上重要结论在题目中如果能直接使用则可以大大提升做题速度,后面证明中作辅助线的方法在某些大题中可以提供思路和线索.对于一些反比例相关的压轴题还是比较有用的.