中考数学方法——抓住题眼 从容应对压轴题

近几年各地中考的数学压轴题，经常出现有关坐标与几何存在性的问题，特别是结合初中二次函数的知识，大部分学生都感觉特别难，因为这种题型对数学知识覆盖面较广，综合性较强，出现的中考题构思非常精巧，解题方法灵活，对学生的分析问题和解决问题的能力要求较高，真正区分出学生数学思维的优劣，所以近几年这部分是中考的"热点"，更是 难点。如果你能抓住"题眼"，那么难题将不再是难题了！

今天利用一道中考题，让大家明白：压轴题并不可怕，大家一定要树立信心，希望今年参加中考的学生，取得优异的成绩。

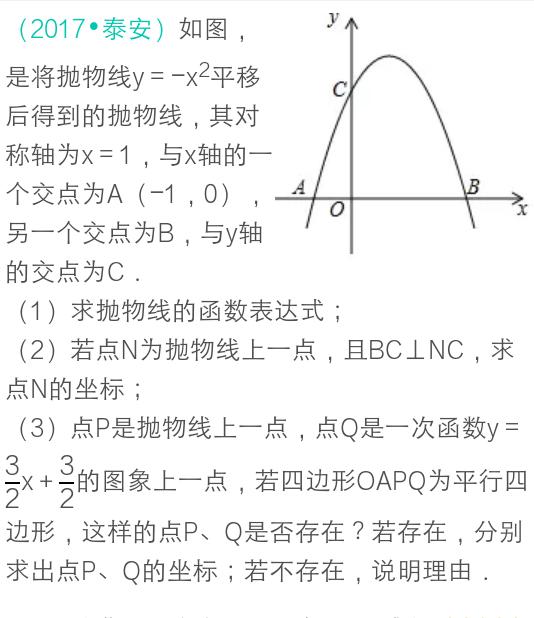
大家看到这道中考题时，我认为首先是要整体感知把握，看图像马上想到考察的就是二次函数，其次要边看边标记题目的条件和要求，最后深入思考每个问题需要用到什么条件？找到的题目条件如何运用到解题当中？

（1）已知抛物线的对称轴x=1和A（-1,0），平移可知a=-1,因而可以设出顶点式，利用待定系数法求函数解析式。也可以根据A点在x轴上，利用对称性得到B点坐标（3,0），直接用交点式得其二次函数表达式。

（2）结合（1）知B和C的坐标，得OB=OC,所以△OBC是等腰直角三角形，过点N作NH⊥y轴，垂足是H，设点N纵坐标是（a，﹣a2+2a+3），根据CH=NH即可列方程求解；

（3）四边形OAPQ是平行四边形，则PQ=OA=1，且PQ∥OA，设P（t，﹣t2+2t+3），带入一次函数表达式求解即可。

以上三问黑体字可以说是解决问题的关键，也就是所谓的"题眼"另外第（3）问在审题上要注意，四边形OAPQ四点的顺序是一定的，从而得到PQ∥OA。上答案大家看看！