例:如图,在矩形ABCD中,延长CB至点E,使CE=CA,点F为AE中点,连结BF、DF。求证:BF⊥DF
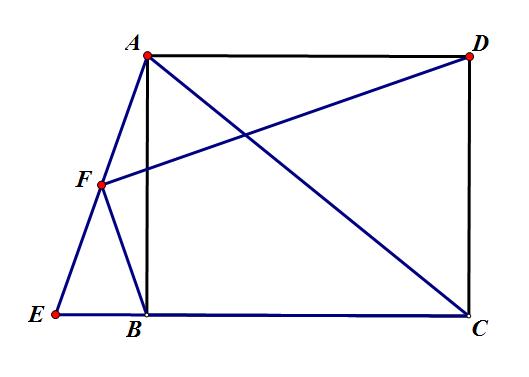
题目图形
方法1:连接BD,延长BF、DA交于点M。
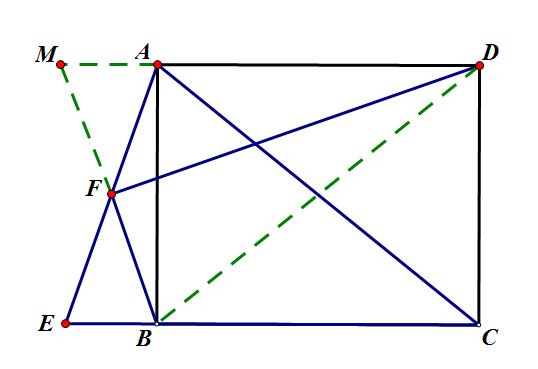

方法1
方法2:连接CF,
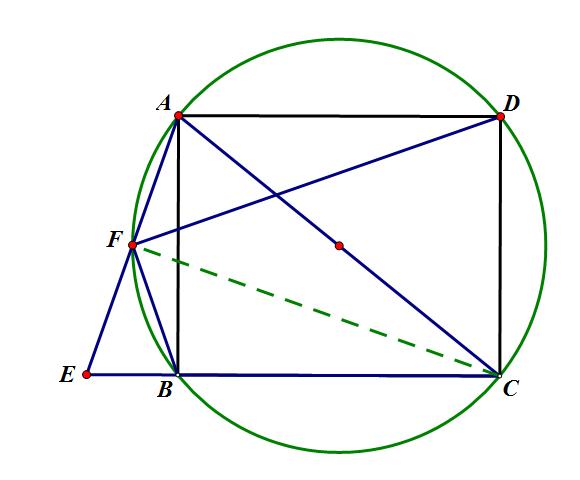

方法2
补充说明:1.四点共圆概概念:如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
2.四点共圆性质:(1)共圆的四个点所连成同侧共底的两个三角形的顶角相等;(2)圆内接四边形的对角互补;(3)圆内接四边形的外角等于内对角。
3.四点共圆判定:(1)若平面上四点连成四边形的对角互补或一个外角等于其内对角,那么这四点共圆;
(2) 把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角相等,从而即可肯定这四点共圆。
 加载中,请稍侯......
加载中,请稍侯......
精彩评论