一元二次方程在解几何问题中的应用

一元二次方程是解数学问题的有力工具，许多数学问题都可转化为解一元二次方程、研究一元二次方程根的性质等而获解。

从本质上讲，列二次方程解应用题与前面我们已经学过的列一元二次方程解应用题没有区别，通常都要经过设、列、解、答等四个步骤，解题的关键是寻找实际问题中的等量关系。特别需要注意的是，列出的一元二次方程一般会有两个不同的实数根，所以在检验时应特别注意，很可能其中有不符合实际问题的根，必须舍去。

今天我就一元二次方程在解几何问题中的应用做一个专题。

解题思路：对于（2），利用“腰相等”建立方程，解题的关键是分类讨论.

【例2】如图，已知在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点E在直角边AC上（点E与A，C两点均不重合）.

（1）若点F在斜边AB上，且EF平分Rt△ABC的周长，设AE＝x，试用x的代数式表示△AEF的面积；

（2）若点F在折线ABC上移动，试问：是否存在直线EF将Rt△ABC的周长和面积同时平分？若存在直线EF，则求出AE的长；若不存在直线EF，请说明理由.

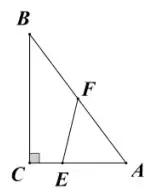
解题思路：几何计算问题代数化，通过定量分析回答是否存在这样的直线EF，将线段的计算转化为解方程.

【例3】 已知：如图1，在Rt△ACB中，∠C＝90°，AC＝4cm，BC＝3cm，点P由点B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由点A出发沿AC方向向点C匀速运动，速度为2 cm/s .连结PQ.若设运动的时间为t（s）（0＜t＜2），解答下列问题：

（1）当t为何值时，PQ∥BC？

（2）设△AQP的面积为y，求y与t之间的函数关系式；

（3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；

（4）如图2，连结PC，并把△PQC沿QC翻折，得到四边形PQP´C，那么是否存在某一时刻t，使四边形PQP´C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由.

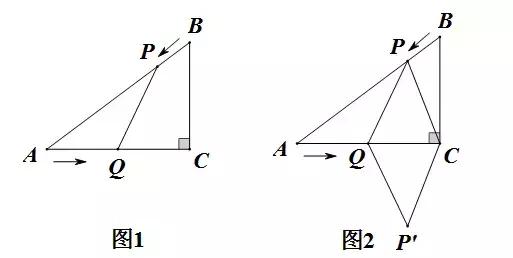
解题思路：对于（3），先求出PQ平分Rt△ACB周长时t的值，再看求出t的值是否满足由面积关系建立的方程

跃跃欲试：下面给出几个练习题，大家可以做一下，答案下期公布。