高考中利用导数研究函数问题时，恒成立和最值是个中心点，这个时候常常需要构造函数，并求导研究函数的单调性来解决问题，题目特点不同，构造方法不同，构造函数的方法有很多，这里只是列举了几个例子，希望能够达到开拓思路，举一反三的目的。

方法一：“比较法”构造函数

技法二：“拆分法”构造函数

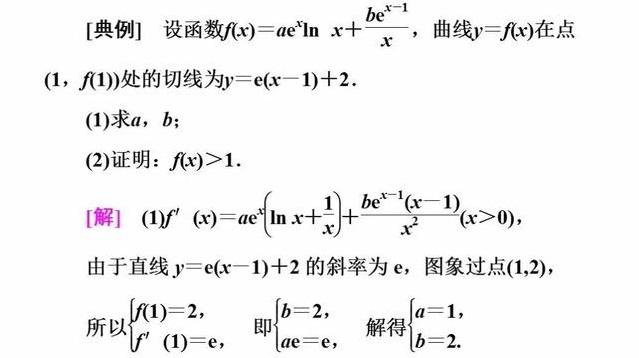
技法三：“换元法”构造函数

方法四：二次（多次）构造函数法

高中数学中，导数主要用来研究函数，高考中导数与函数的问题一直是热点，导数研究函数主要是：研究函数最值（利用单调性）；研究函数零点（利用求导研究单调性，研究函数图像，研究最值）；研究不等式（构造函数研究最值恒成立问题）。