三角形中的“中点模型”方法总结（重点知识）

三角形是初中数学必考的重要知识点，学好三角形是学好初中几何的关键。而在三角形相关题目中出现最多的就是中点和角平分线，今天我们来总结一下，遇到中点都有那些处理方法。掌握了这几种方法，应对三角形相关题目时，同学们将得心应手！

类型一 倍长中线或类中线

类型二 遇等腰三角形，构造“三线合一”

类型三 遇RT三角形斜边的中点，构造斜边的中线

类型四 遇多个中点，构造中位线

例题分析：

1、遇到中点，常想倍长中线法

例题分析：

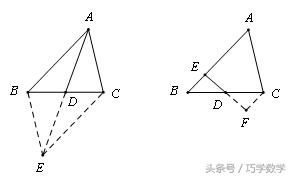
如图，在△ABC中，AB=10，AC=6，那么BC边上的中线AD的取值范围是。

解:

延长AD到E,使DE=AD,连接BE.

∵ BD=CD AD=DE ∠CDA=∠BDE

∴ △ADC≌△EDB (两边及其夹角对应相等的两个三角形全等)

∴ AC=BE (全等三角形的对应边相等)

∵ AC=BE AC=6

∴ BE=6

∵ BE=6 AB=10 AB-BE＜AE

∴ 4＜AE

∵ BE=6 AB=10 AE＜AB+BE

∴ AE＜16

∵ 4＜AE AE＜16

∴ 4＜AE＜16

∵ 4＜AE＜16 AD=12×AE

∴ 2＜AD＜8

2、遇等腰三角形，构造“三线合一”

如图，△ABC是等腰直角三角形，AB=AC，D是斜边BC的中点，E. F分别是AB、AC边上的点，且DE⊥DF.

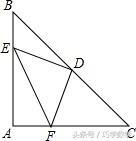
请说明：DE=DF；

证明：连接AD,

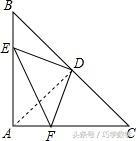
∵等腰直角三角形ABC，

∴∠C=∠B=45°，

∵D为BC的中点，

∴AD⊥BC，AD=BD=DC，AD平分∠BAC，

∴∠DAC=∠BAD=45∘=∠B,∠ADC=90°，

∵DE⊥DF，

∴∠EDF=90°，

∴∠ADF+∠FDC=90°,∠FDC+∠BDE=90°，

∴∠BDE=∠ADF，

在△BDE和△ADF中

∠B=∠DAF

BD=AD

∠BDE=∠ADF，

∴△BDE≌△ADF，

∴DE=DF.

3、遇多个中点，构造中位线

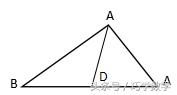
如图,四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=4,DC=2,则MN的长不可能是( )

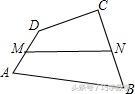
A. 3 B. 2.5 C. 2 D. 1.5

解：如图,连接BD,取BD的中点G,连接MG、NG,

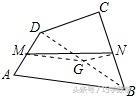
∵点M，N分别是AD、BC的中点，

∴MG是△ABD的中位线，NG是△BCD的中位线，

∴AB=2MG，DC=2NG，

∴AB+DC=2(MG+NG)，

由三角形的三边关系，MG+NG>MN，

∴AB+DC>2MN，

∴MN<12(AB+DC)，

∴MN<3；

故选：A.