简单多面体外接球问题是立体几何中的难点重要考点,此类问题的实质是解决球的半径R和确定球心的位置问题,其中确定球心的位置是关键.
由球的定义确定球心
在空间,如果一个定点与一个简单多面体的所
有顶点的距离都相等,那么这个定点就是该简单多
面体的外接球的球心.
由上述性质,可以得到确定简单多面体外接球
的球心的如下结论.
结论 1 正方体或长方体的外接球的球心是其
体对角线的中点.
结论 2 正棱柱的外接球的球心是上下底面中
心的连线的中点.
结论 3 直三棱柱的外接球的球心是上下底面
三角形外心的连线的中点.
结论 4 正棱锥的外接球的球心是在其高上,
具体位置可通过计算找到.
结论 5 若棱锥的顶点可构成共斜边的直角三
角形,则公共斜边的中点就是其外接球的球心.
一、出现“墙角”结构利用补形知识,联系长方体。

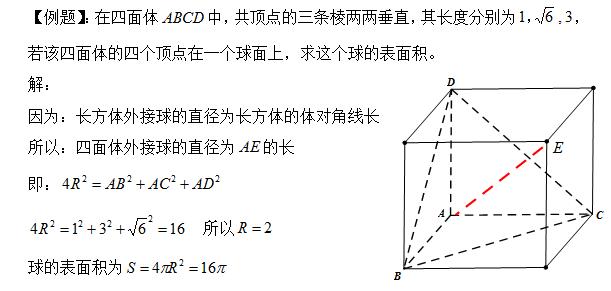
二、出现两个垂直关系,利用直角三角形结论。
【原理】:直角三角形斜边中线等于斜边一半。球心为直角三角形斜边中点。

【总结】斜边一般为四面体中除了直角顶点以外的两个点连线。
二、出现多个垂直关系时建立空间直角坐标系,利用向量知识求解
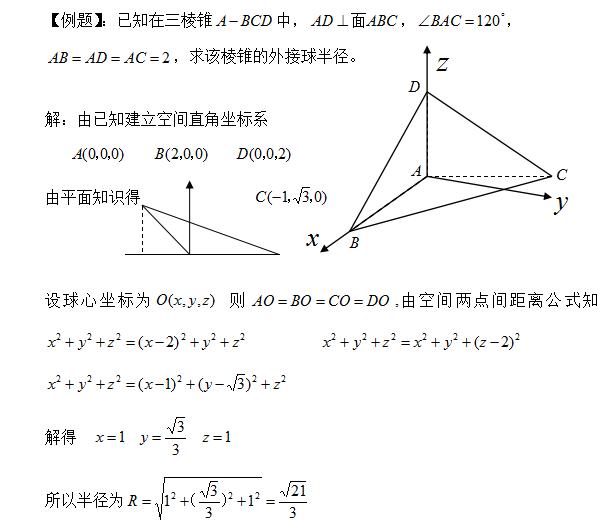
【结论】:空间两点间距离公式:
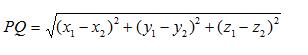
二、四面体是正四面体
外接球与内切球的圆心为正四面体高上的一个点,
根据勾股定理知,假设正四面体的边长为时,它的外接球半径为
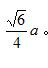
思考题
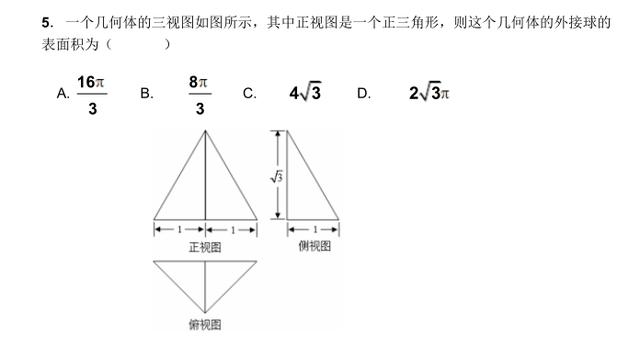
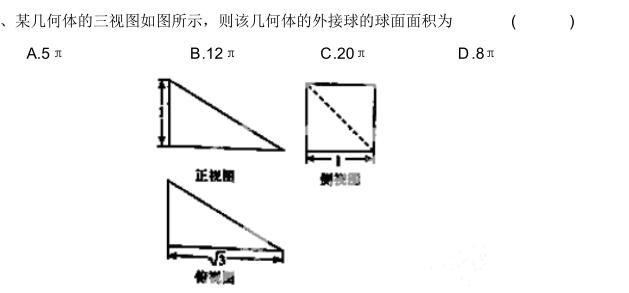
 加载中,请稍侯......
加载中,请稍侯......
精彩评论