教你解与二次函数有关的分类讨论综合问题

下面一起来先看一道中考真题，与二次函数有关的分类讨论综合题型，典型例题分析1：

如图所示，在平面直角坐标系xoy中，正方形OABC的边长为2cm，点A、C分别在y轴的负半轴和x轴的正半轴上，抛物线y=ax2+bx+c经过点A、B和D（4，-2/3）.

（1）求抛物线的表达式.

（2）如果点P由点A出发沿AB边以2cm/s的速度向点B运动，同时点Q由点B出发，沿BC边以1cm/s的速度向点C运动，当其中一点到达终点时，另一点也随之停止运动。设S=PQ2（cm2）.

①试求出S与运动时间t之间的函数关系式，并写出t的取值范围；

②当S取5/4时，在抛物线上是否存在点R，使得以点P、B、Q、R为顶点的四边形是平行四边形？如果存在，求出R点的坐标；如果不存在，请说明理由.

（3）在抛物线的对称轴上求点M，使得M到D、A的距离之差最大，求出点M的坐标.

考点分析：

二次函数综合题；待定系数法求一次函数解析式；二次函数图象上点的坐标特征；待定系数法求二次函数解析式；勾股定理；平行四边形的性质。

题干分析：

（1）设抛物线的解析式是y=ax2+bx+c，求出A、B、D的坐标代入即可；

（2）①由勾股定理即可求出，②假设存在点R，可构成以P、B、R、Q为顶点的平行四边形，求出P、Q的坐标，再分为三种情况：A、B、C即可根据平行四边形的性质求出R的坐标．

（3）A关于抛物线的对称轴的对称点为B，过B、D的直线与抛物线的对称轴的交点为所求M，求出直线BD的解析式，把抛物线的对称轴x=1代入即可求出M的坐标。

解题反思：

本题主要考查了用待定系数法求一次函数和二次函数的解析式，勾股定理，平行四边形的性质，二次函数图象上点的坐标特征等知识点，解此题的关键是综合运用这些知识进行计算．此题综合性强，是一道难度较大的题目。

在中考数学中，二次函数与分类讨论本身就是属于难点较大、综合性较强的知识内容，他们更是每年中考数学的热门考点。因此，在中考数学中，一旦把二次函数与分类讨论结合在一起，就加大题目的难度，对考生的解题能力提出了挑战。

数学学习讲究思维性，分类讨论更是体现这种思维性，体现了化整为零、积零为整的思想与归类整理的方法，是一种重要的数学思想，同时也是一种重要的解题策略。

在平时的数学学习过程中，大家一定要清醒的认识到一点：中考数学不仅仅考查的知识点、定理、公式，更加考查大家的知识运用能力，解决问题能力等。

与二次函数有关的分类讨论综合题型，典型例题分析2：

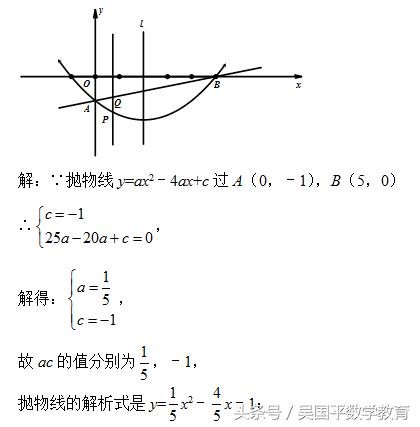
如图，抛物线y=ax2﹣4ax+c（a≠0）经过A（0，﹣1），B（5，0）两点，点P是抛物线上的一个动点，且位于直线AB的下方（不与A，B重合），过点P作直线PQ⊥x轴，交AB于点Q，设点P的横坐标为m．

（1）求a，c的值；

（2）设PQ的长为S，求S与m的函数关系式，写出m的取值范围；

（3）以PQ为直径的圆与抛物线的对称轴l有哪些位置关系？并写出对应的m取值范围．（不必写过程）

考点分析：

二次函数综合题。

题干分析：

（1）利用待定系数法把点A、B的坐标代入抛物线表达式解二元一次方程组即可；

（2）先求出直线AB的解析式，然后分别求出点P与点Q的坐标，则PQ的长度S就等于点Q的纵坐标减去点P的纵坐标，然后整理即可；

（3）根据直线与圆的位置关系有相离、相切与相交共三种情况，又点P可以在对称轴左边也可以在对称轴右边，进行讨论列式求解即可．

解题反思：

本题考查了待定系数法，直线与二次函数相交的问题，直线与圆的位置关系，综合性较强，对同学们的能力要求较高，（3）中要注意分点P有在对称轴左边与右边的两种情况，容易漏解而导致出错。

在解决与函数相关的综合问题过程中，我们经常会用到分类讨论等数学思想，面对此类问题，大家一定不要紧张，千万记住在解决问题过程中，认真仔细的对问题各种情况加以分类，并逐类求解，然后综合得解，拿到分数。