行测数量关系备考：时针问题

时钟问题其实是行程问题的一种，主要研究钟面上时针与分针的相遇追击问题以及坏钟时间与标准时间的关系。根据解题方法的不同，时钟问题可以细分为钟面问题和坏钟问题两大类。中公教育专家就将这两种问题的解答方法给各位考生做一下讲解：

知识点一：钟面问题

要快速解时针问题，必须要了解一些基础知识：

钟面问题经常围绕着时针与分针重合、垂直(夹角为90°或270°)、成直线(夹角为180°)、成一定角度等展开。

1.已知时间点求角度

(1)整点时，时针与分针的夹角画出钟面示意图即可得出。

例题1： 清晨5点时，时钟的时针和分针的夹角是多少度?

中公解析：画出示意图，可知夹角为5格，即5×30°=150度。

(2)非整点时，则需根据整点情况，再结合两针走过的角度之间的关系根据示意图求解。

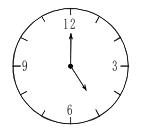
例题2： 在时钟盘面上，1点45分时的时针与分针之间的夹角是多少?

中公解析：画出示意图，1∶00到1∶45分，时针走的度数为0.5°×45=22.5°。

9点到1点之间有4个格，角度为30°×4=120°。

所以夹角为120°+22.5°=142.5°。

2.已知时针分针成某一角度求时间

这一类问题即相当于行程问题中的追及问题。追及速度=5.5°/分钟，追及路程=角度差。

这类问题的解题流程如下：

(1)找出两针转动的角度差;

(2)利用公式：角度差÷5.5°/分钟=分钟数，求出所需的时间。:

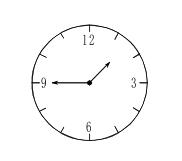
例3：4点多少分的时候时针和分针第一次重合?

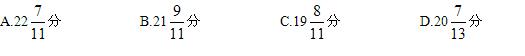
中公解析：此题答案为B。画出示意图，4点时，两针夹角为4×30°=120°。

4点时，时针在分针前面，第一次重合即分针追上时针，即分针比时针多走120°，则需要120÷5.5=

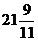
分钟。

3.时针和分针等距分列数字两旁

这类问题可转化为相遇问题来求解，这种情况下，速度和为6.5°/分钟，两针转过的角度和=路程和。

这类问题的解题流程如下：

(1)找出两针转动的角度和;

(2)利用公式：角度和÷6.5°/分钟=分钟数，求出所用的时间。

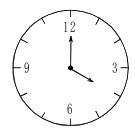
例题4： 钟面上3点几分时，时针和分针离“3”的距离相等，并且在“3”的两旁?

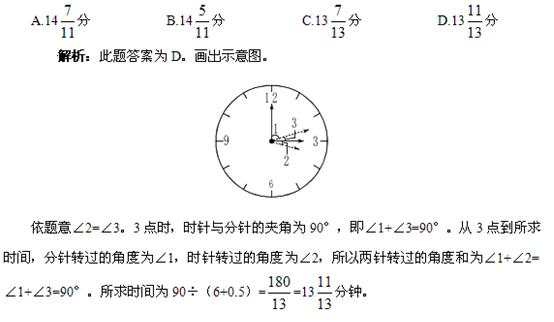
知识点二：坏钟问题

一个坏钟(或坏表)，每小时比标准时间快(或慢)N分钟，T1时刻将这个钟与标准时间对准。当这个钟的时间显示为T2时，标准时间是多少?

这类涉及坏钟时间与标准时间之间的问题，统称为坏钟问题，解题时将坏钟时间与标准时间的快慢关系转化为比例问题求解。

坏钟时间与标准时间的比例关系：每小时快N分钟，则标准时间的1小时即60分钟中，快钟走(60+N)分钟，快钟时间∶标准时间=(60+N)∶60。

假设快钟显示的T1到T2这段时间为x分钟，标准时间走了y分钟，则根据(60+N)：60=x:y,此时可求出y=

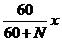
，从而求出T2的实际时间。

例5：有一个钟，每小时慢3分钟，早晨4点30分的时候，把钟对准了标准时间，则钟走到当天上午10点50分的时候，标准时间是多少?

A.11点整 B. 11点5分 C.11点10分 D.11点15分

中公解析：答案选C。每小时慢3分钟，即坏钟时间：标准时间=57:60。慢钟从4点30分走到10点50分，一共走了6小时20分，总共380分钟，假设标准时间走了x分钟，那么x=

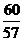
×380=400分钟。说明标准时间比慢钟显示时间快400-380=20分钟，标准时间应为10点50分往后推20分钟，即11点10分。