初中数学圆的相关性质

考点一圆的概念及其性质

1．圆的概念有两种方式

(1)在一个平面内，线段OP绕它固定的一个端点O旋转一周，另一个端点P所经过的封闭曲线叫做圆．定点O叫做圆心，线段OP叫做半径；

(2)圆是到定点的距离等于定长的点的集合．

2．圆的对称性

(1)圆是轴对称图形，经过圆心的每一条直线都是它的对称轴；

(2)圆是以圆心为对称中心的中心对称图形；

(3)圆绕圆心旋转任意角度，都能和原来的图形重合，这就是圆的旋转不变性．

考点二圆的性质及定理

1．性质：垂直于弦的直径平分这条弦，并且平分弦所对的弧．

如图，CD是⊙O的直径，AB为弦，CD⊥AB，垂足为E，则AE＝EB，弧AD＝弧BD，弧AC＝弧BC

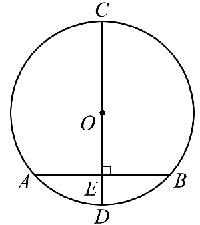
2．定理1：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧．

定理2：平分弧的直径垂直平分弧所对的弦．

温馨提示：

平分弦的直径不一定垂直于弦，只有被平分的弦不是直径时才互相垂直．

考点三弧、弦、圆心角之间的关系

1．在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等．

2．在同圆或等圆中，如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等，那么它们所对应的其余各对量都相等．

考点四圆心角与圆周角

1．定义：顶点在圆心的角叫做圆心角；顶点在圆上，且两边都与圆相交的角叫做圆周角．

2．圆周角定理：一条弧所对的圆周角等于它所对圆心角的一半．

3．推论1：半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径．

推论2：在同圆或等圆中，同弧或等弧所对的圆周角相等；相等的圆周角所对的弧也相等．

温馨提示：

1．圆周角定理的意义在于把圆周角和圆心角这两类不同的角联系在一起．

2．同一条弧所对的圆周角相等；同一条弦所对的圆周角相等或互补．

3．当已知条件中有直径时，常常作直径所对的圆周角，这是圆中常添加的辅助线．

考点五圆内接四边形性质定理

1．性质定理1：圆内接四边形的对角互补．

2．性质定理2：圆内接四边形的外角等于它的内对角．

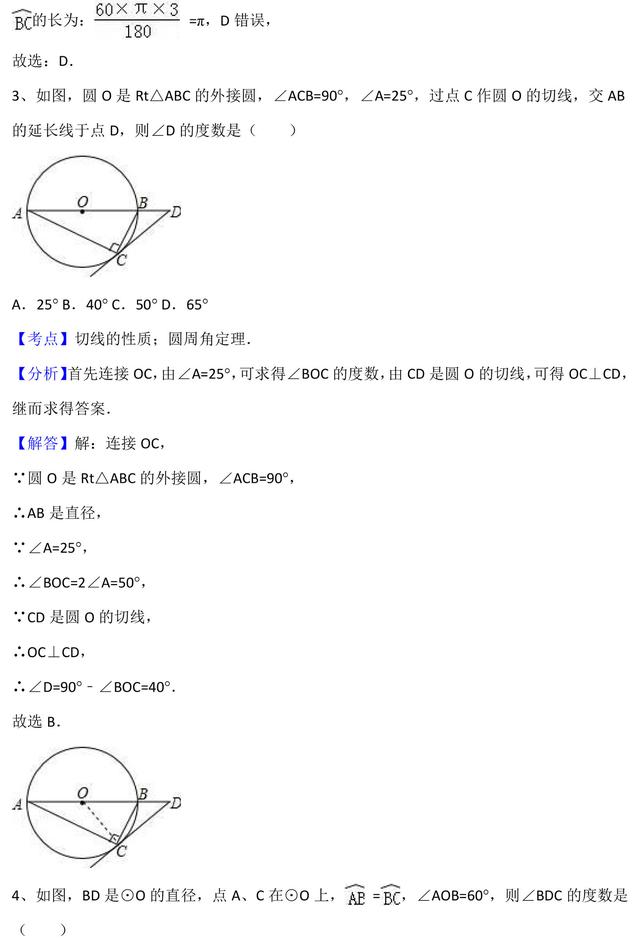
如图，四边形ABCD内接于⊙O，则∠A＋∠BCD＝∠B＋∠D＝180°，∠DCE＝∠A．