相似三角形三点定形证明和全等三角形辅助线证明

方法一：直接寻求相似三角形

只要根据题目给定的条件寻找出线段成比例，或者角相等利用判定定理直接找出来.

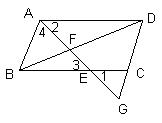
例1、如图：点G在平行四边形ABCD的边DC的延长线上,AG交BC、BD于点E、F，则△AGD∽△EGC ∽△EAB。

分析：关键在找“角相等”，除已知条件中已明确给出的以外，还应结合具体的图形，利用公共角、对顶角及由平行线产生的一系列相等的角。本例除公共角∠G外,由BC∥AD可得∠1=∠2，所以△AGD∽△EGC。再∠1=∠2（对顶角），由AB∥DG可得∠4=∠G，所以△EGC∽△EAB。

评注：（1）证明三角形相似的首选方法是“两个角对应相等的两个三角形相似”。（2）找到两个三角形中有两对角对应相等，便可按对应顶点的顺序准确地把这一对相似三角形记下来。