一、列方程解应用题

例题：“5·12”汶川大地震后，灾区急需大量帐篷．某服装厂原有4条成衣生产线和5条童装生产线，工厂决定转产，计划用3天时间赶制1000顶帐篷支援灾区．若启用1条成衣生产线和2条童装生产线，一天可以生产帐篷105顶；若启用2条成衣生产线和3条童装生产线，一天可生产帐篷178顶。问：

(1)每条成衣生产线和童装生产线每天生产帐篷各多少顶?

(2)工厂满负荷全面转产，是否可以如期完成任务?如果你是厂长，你会怎样体现你的社会责任感？

参考答案：设每条成衣生产线和童装生产线平均每天生产帐篷x、y顶，则有X+2Y=105，2X+3Y=178，解得X=41，Y=32

二、列方不等式解应用题

例题：北京奥运会帆船比赛将在青岛国际帆船中心举行．观看帆船比赛的船票分为两种：A种船票600元／张，B种船票120元／张．某旅行社要为一个旅行团代购部分船票，在购票费不超过5000元的情况下，购买A、B两种船票共15张，要求A种船票的数量不少于B种船票数量的一半．若设购买A种船票x张，请你解答下列问题：

(1)共有几种符合题意的购票方案?写出解答过程；

(2)根据计算判断：哪种购票方案更省钱?

参考答案：根据题意列出不等式X≥（15－X）/2；600X+120（15－X）≤5000，解得5≤X≤20/3，满足条件的为X=5或X=6，带入购票方案，得出方案一的费用为600×5+120×10=4200元，方案二的费用为60×6+120×9=4680元，所以方案一(A种票5张，B种票10张)更省钱。

三、用一次函数解应用题

例题：某公司在A、B两地分别库存挖掘机16台和12台，现在运往甲、乙两地支援建设，其中甲地需要15台，乙地需要13台．从A地运一台到甲、乙两地的费用分别是500元和400元；从B地运一台到甲、乙两地的费用分别是300元和600元．设从A地运往甲地x台挖掘机，运这批挖掘机的总费用为y元。问：公司应设计怎样的方案，能使运这批挖掘机的总费用最省?

参考答案：根据题意得出Y=500X+400(16-X)+300(15-X)+600(X-3)=400X+9100，因为X-3≥0且15-X≥0，得出3≤X≤5.因为即又y随x增大而增大，所以当x=3时，能使运这批挖掘机的总费用最省。运送方案是A地的挖掘机运往甲地3台，运往乙地13台；B地的挖掘地运往甲地12台，运往乙地0台。

四、用二次函数解应用题

例题：研究所对某种新型产品的产销情况进行了研究，为了投资商在甲、乙两地生产并销售该产品提供了如下成果：第一年的年产量为x（吨）时，所需的全部费用y（万元）与x满足关系式：

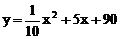
投入市场后当年能全部售出，且在甲、乙两地每吨的售价、（万元）均与x满足一次函数关系。（注：年利润=年销售额-全部费用）

（1）成果表明，在甲地生产并销售x吨时，P甲= —1/20X+14,请你用含x的代数式表示甲地当年的年销售额，并求年利润W甲（万元）与x之间的函数关系式；

（2）成果表明，在乙地生产并销售x吨时，P甲= —1/10X+n（n为常数），且在乙地当年的最大年利润为35万元。试确定n的值；

（3）受资金、生产能力等多种因素的影响，某投资商计划第一年生产并销售该产品18吨，根据（1），（2）中的结果，请你通过计算帮他决策，选择在甲地还是乙地产销才能获得较大的年利润？

......

其它常考的五类题型分别是：画几何图形解应用题、方程与不等式结合解应用题、不等式与函数结合型解应用题、不等式与统计结合解应用题，以及方程、不等式、函数结合型