小学数学计算学习：巧用乘法分配律

逆用乘法分配律进行计算时，要找出几个乘法算式中相同的乘数，有时需要对算式进行一些变化，才能找到几个乘法算式中的相同乘数。

（1）计算1999+999×999，在此题中直接进行计算会稍麻烦，我们可以把1999进行简单变化，即把1999改写成1000+999，然后把999+999×999逆用乘法分配律进行计算。

（2）计算88×91 + 11×72，此题中的两个乘法算式中没有相同的乘数，所以不能直接逆用乘法分配律进行简算，但通过观察发现第一个乘法算式中的88是11的倍数，可以把88改写成11×8，这样就找到了相同的乘数，从而逆用乘法分配律进行简算。

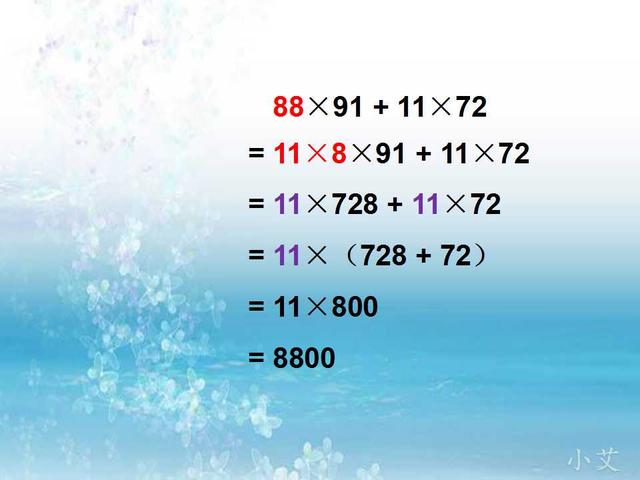
既然88是11的倍数，所以此题也可以把第二个乘法算式中的11改写成88。

再比如计算9999×2222+3333×3334，按照上面的方法，可以把9999变成3333×3。

（3）有些题看似可以运用乘法分配律进行简算，其实不然，比如计算2009×20082008 - 2008×20092009。

观察此题发现，两个乘法算式中都有类似2008、2009形式的数，还发现20082008是2008的倍数，即20082008=2008×10001，同理20092009=2009×10001，所以此题对乘数稍加变形就可以解决问题了。