数学丨全等三角形原来如此简单，期末之前一起来学习、巩固！

壹：知识精讲

1．全等形与全等三角形

（1）全等形：能够完全重合的两个图形叫做全等形．

（2）全等三角形：能够完全重合的三角形就是全等三角形．

2．全等三角形的性质

（1）性质：全等三角形的对应边相等，对应角相等．

（2）全等三角形对应边上的中线相等，对应边上的高相等，对应角的角平分线相等，周长、面积相等．

3．全等三角形的判定

（1）边角边定理(SAS)：两边和它们的夹角对应相等的两个三角形全等．

（2）角边角定理(ASA)：两角和它们的夹边对应相等的两个三角形全等．

（3）边边边定理(SSS)：三边对应相等的两个三角形全等．

（4）角角边定理(AAS)：两个角和其中一个角的对边对应相等的两个三角形全等．

（5）斜边、直角边定理(HL)：斜边和一条直角边对应相等的两个直角三角形全等．

4．角平分线

（1）性质：角平分线上的点到角的两边距离相等．

（2）判定：到角的两边距离相等的点在角的平分线上．

贰：解题技巧

1．倍长中线法构造全等

如图，AD为△ ABC的中线，延长AD至E，连接EB(EC)，则可得到一对全等三角形．

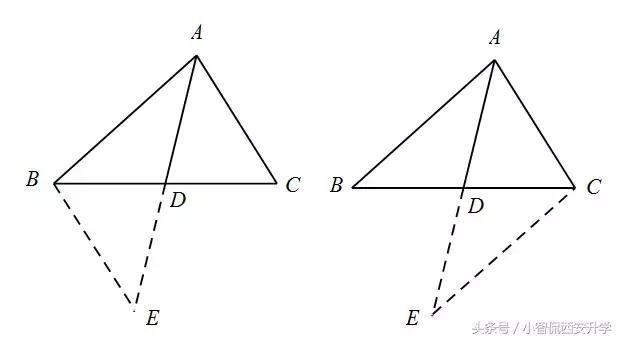
2．角分线辅助线

角平分线是天然的对称模型，一般情况下，有下列三种作辅助线的方式：

①由角平分线上的一点向角的两边作垂线，

②过角平分线上的一点作角平分线的垂线，从而形成等腰三角形，

③OA=OB，这种对称的图形应用得也较为普遍，

3．截长补短法

当已知条件出现求证线段等于另外两线段和、差时，可以选用截长补短法．

4．手拉手模型

5．一线三等角的全等

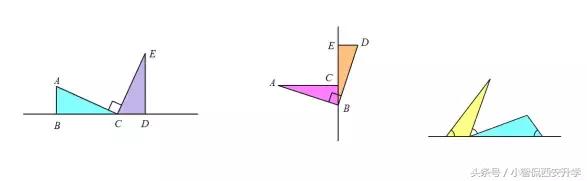
叁：易错点辨析

（1）边边角不能确定三角形全等．

（2）角角角只能确定三角形的形状，不能确定三角形的大小．

亲爱的同学们，看了朱老师的总结是不觉得原来全等三角形是这么的简单，原来做起题目来是这么简单，原来学习是这么的简单。那么以后遇到全等三角形这种题型可一定稳稳的拿下分。