基本要求：了解图形的旋转，理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质；会识别中心对称图形

略高要求：能按要求作出简单平面图形旋转后的图形，能依据旋转前后的图形，指出旋转中心和旋转角．

较高要求：能运用旋转的知识解决简单的计算问题；能运用旋转的知识进行图案设计．

开始讲课

开始讲解知识点：

一、旋转有关概念

旋转：把一个图形绕着某一点转动一个角度的图形变换叫做旋转，点叫做旋转中心，转动的角叫做旋转角，如果图形上的点经过旋转变为点，那么这两个点叫做这个旋转的的对应点．(如图1)

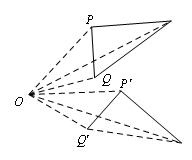
图1

注意：⑴研究旋转问题应把握两个元素：旋转中心与旋转角．

⑵每一组对应点所构成的旋转角相等．

旋转的性质：

①旋转后的图形与原图形是全等的；(进而得到相等的线段、相等的角)

②旋转前后两个图形对应点到旋转中心的距离相等；(进而得到等腰三角形)

③对应点与旋转中心所连线段的夹角都等于旋转角；(若特殊角则得到等边三角形、等腰直角三角形)

旋转作图的基本步骤：

由旋转的性质可知，旋转作图必须具备两个重要条件：

⑴旋转中心；⑵旋转方向及旋转角度．

具体步骤分以下几步：

连：即连接图形中每一个关键点与旋转中心．

转：即把连线按要求绕旋转中心转过一定角度(作旋转角)

截：即在角的另一边上截取关键点到旋转中心的距离，得到各点的对应点．

连：即连接所得到的各点．

二、中心对称

中心对称的有关概念：

把一个图形绕着某一点旋转

，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做中心对称点，这两个图形中的对应点叫做关于中心的对称点(如图2)

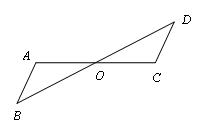
图2

注意：

⑴两个图形成中心对称是旋转角为定角(180度)的旋转问题，它是一种特殊的旋转，反映的是两个图形的一种特殊关系．

⑵中心对称阐明的是两个图形的特殊位置关系．

中心对称的特征：

关于中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心所平分．

关于中心对称的两个图形是全等图形．

关于中心对称的两个图形，对应线段平行(或在同一直线上)且相等．

如果连接两个图形的对应点的线段都经过某一点，并且被这一点平分，那么这两个图形一定关于这一点成中心对称．

中心对称图形：

把一个图形绕着某一点旋转180度，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．(如图⑶)

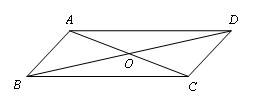
图3

中心对称与中心对称图形的区别与联系：

中心对称是指两个图形的关系，中心对称图形是指具有某种性质的一个图形．若把中心对称图形的两个部分分别看作两个图形，则他们成中心对称；若把中心对称的两个图形看作一个整体，则成为中心对称图形．

关于原点对称的点的坐标特征：

两个点关于原点对称时，他们坐标符号相反，反过来，只要两个点的坐标符号相反，则两个点关于原点对称．

中心对称图形与旋转对称图形的比较：

中心对称图形与轴对称图形比较：

学好数学，要多做典型题

现在来做几道练习题巩固一下：

1、下列图形中，绕某个点旋转能与自身重合的有( )

①正方形 ②长方形 ③等边三角形 ④线段 ⑤角

A．5个 B．2个 C．3个 D．4个

2、在下列四种图形变换中，本题图案不包含的变换是( )

①中心对称　②旋转　③轴对称　 ④平移

A．①② B．②③　C．③④　D．①④

第2题图片