初二数学《实数》

实数的概念：有理数和无理数，统称为实数，即实数包括有理数和无理数。

实数的分类：

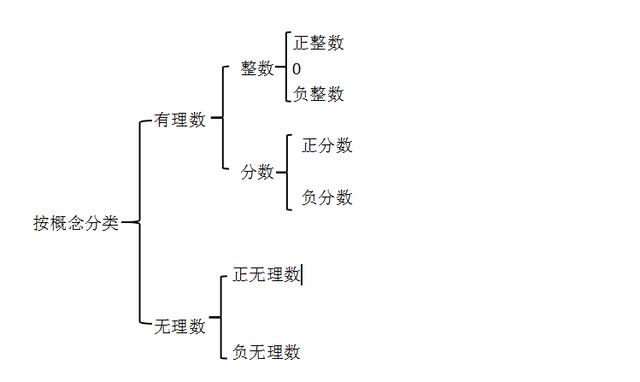
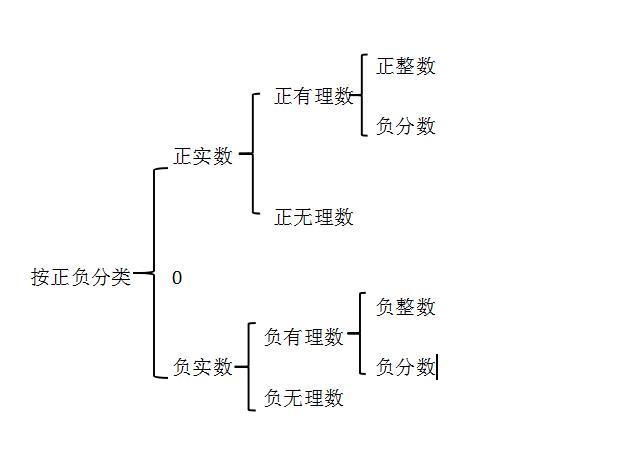
有理数与无理数的区别：.有理数是有限小数或无限循环小数。而无理数是无限不循环小数。所有的有理数都能写成分数的形式，整数可以看成分母是1的分数，而无理数不能写成分数的形式。

初中阶段所学的无理数主要包含以下几种：

1、特殊意义的数，如圆周率π及含有π的一些数。

2、开方开不尽的数的方根。

3、特殊结构的无限不循环小数，如2.010010001…

无理数必须同时满足“无限”和“不循环”这两个条件，不要误以为除不尽的数也是无理数，例如22/7，它除不尽，但它是循环小数，所以它不是无理数。

比较两个实数的大小的常用方法：

1、利用数轴，在数轴上表示的数，右边的数总比左边的数大。

2、用估算的方法，求出无理数的近似值，或利用计算器计算出无理数的近似值，再比较两数的大小。

除以上方法，还有平方法、倒数法、比商法等。

要去掉绝对值符号，必须考虑绝对值内的数或式的符号

对于实数的运算：

1、要熟练的把有理数的运算律和运算法则准确的运用到实数预算中。

2、涉及无理数的计算，会根据问题的要求，取其近似值再计算，注意取各无理数的近似值时，要比最后结果要求的精确度多保留一位。

求无理数整数部分的方法：要确定无理数根号m的整数部分，先要找到根号m在哪两个连续整数之间,找出m在哪两个连续的完全平方数之间,再求这两个完全平方数的算术平方根，根据最小的算术平方根就是根号m的整数部分。而小数部分则可以表示为根号m减去整数部分的形式。