解三角形问题中,边角关系图形能表示能画出来的都一定要画一画草图,把抽象的问题具体化呈现出来,同时也避免重复读题找已知量,即使解题遇到解不下去的时候,往往有可能从图中联系建议新的关系有助于解题

在学习余弦定理的时候,对夹角的大小及其余弦值的正负零都有作分析,其中也重点强调了勾股定理的使用,看似复杂的余弦定理在联系勾股定理后往往显得就很亲切了,好像看见亲人一样,哈哈,这个人我认识,对,没错,就是这种感觉,继续往下。关系量中使用AD为桥梁,联系已知与未知的一个中介,计算的部分不难,而且经常算的多了,也算是简单的一块儿了吧

拆角的方法还是非常棒的,一个三角形△由高线拆成两个直角三角形,求角A的余弦值就转化成了两个锐角和的余弦值,这种思维方法的妙出就在于把复杂的余弦求值问题,转化为两个容易求的锐角和的余弦值求解,题中所给角B的度数就在提示你,这是一个探索之路,你可以尝试去解答,说不定会很简便哟

面积法也是妙不可言的方法,可以发现好多跟几何有关的问题,面积法往往会发挥无穷的威力,简单易求解就是最大的特征
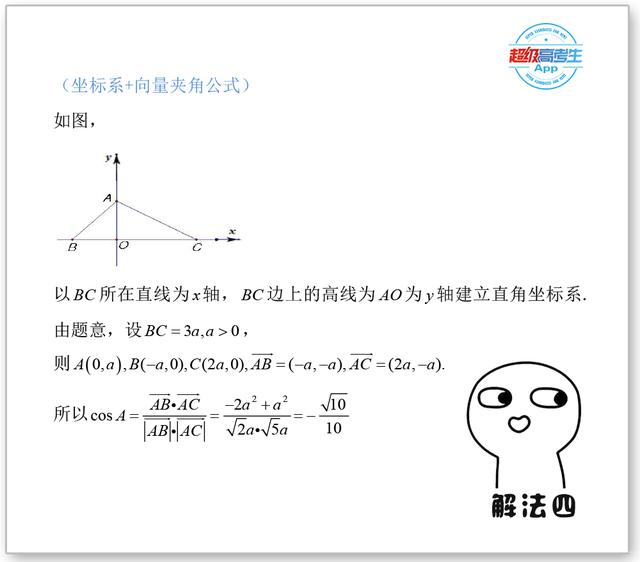
数量积的使用在此题中相对而言会显得稍微繁琐,耗时可能会更长,不是说此法不好,这里给出来就是让大家体会各种方法的思想方法,从而能摘取适合你自己的方法,才是最好的方法
 加载中,请稍侯......
加载中,请稍侯......
精彩评论