中考数学,与二次函数有关的存在性问题,典型例题分析1:
如图,已知抛物线过点A(0,6),B(2,0),C(7,5/2).
(1)求抛物线的解析式;
(2)若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称,求证:∠CFE=∠AFE;
(3)在y轴上是否存在这样的点P,使△AFP与△FDC相似,若有,请求出所有合条件的点P的坐标;若没有,请说明理由.





考点分析:
二次函数综合题;综合题。
题干分析:
(1)设抛物线解析式为y=ax2+bx+c,将A、B、C三点坐标代入,列方程组求抛物线解析式;
(2)求直线AC的解析式,确定E点坐标,根据对称性求F点坐标,分别求直线AF,CF的解析式,确定两直线与x轴的交点坐标,判断两个交点关于抛物线对称轴对称即可;
(3)存在.由∠CFE=∠AFE=∠FAP,△AFP与△FDC相似时,顶点A与顶点F对应,根据△AFP∽△FDC,△AFP∽△FCD,两种情况求P点坐标。
解题反思:
本题考查了二次函数的综合运用.关键是根据已知条件求抛物线解析式,根据抛物线的对称性,相似三角形的知识解题。

与二次函数有关的存在性问题是指判断满足某种条件的事物是否存在的问题。这类问题的知识覆盖面较广,综合性较强,题意构思非常精巧,解题方法灵活,对同学们分析问题和解决问题的能力要求较高,是近几年来各地中考的热点。
与二次函数有关的存在性问题最大特点就是在一定条件下探索发现某些数学结论或规律是否存在的问题.存在性问题探索的方向是明确的,探索的结果有两种:一种是存在;另一种是不存在.由于问题的结论没有明确,而且综合性强,涉及多种数学思想方法。
中考数学,与二次函数有关的存在性问题,典型例题分析2:
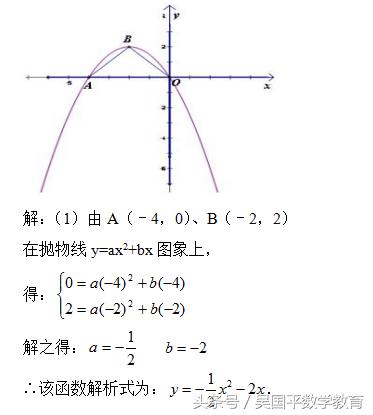
如图,抛物线y=ax2+bx经过点A(﹣4,0)、B(﹣2,2),连接OB、AB,
(1)求该抛物线的解析式.
(2)求证:△OAB是等腰直角三角形.
(3)将△OAB绕点O按逆时针方向旋转135°,得到△OA′B′,写出A′B′的中点P的坐标,试判断点P是否在此抛物线上.
(4)在抛物线上是否存在这样的点M,使得四边形ABOM成直角梯形,若存在,请求出点M坐标及该直角梯形的面积,若不存在,请说明理由.


考点分析:
二次函数综合题;综合题。
题干分析:
(1)将A(﹣4,0)、B(﹣2,2)代入抛物线解析式y=ax2+bx,列方程组求a、b的值即可;
(2)根据所求抛物线解析式求抛物线的顶点坐标,判断三角形的形状;
(3)根据△OAB的形状,旋转方向,旋转角,画出图形,可求A′、B′的坐标,根据中点坐标公式求P的坐标,代入抛物线解析式进行判断;
(4)存在.过点O,作OM∥AB交抛物线于点M,根据△OAB为等腰直角三角形,可求直线OM的解析式,与抛物线解析式联立,可求M点坐标,同理,过点A,作AM′∥OB交抛物线于点M′,联立方程组可求M′的坐标,由图形的特殊性可知,两种情况下,梯形面积相等,根据梯形面积公式求解。
解题反思:
本题考查了二次函数的综合运用.关键是根据题意求抛物线解析式,根据解析式确定图形的特殊性。
大家要记住解与二次函数有关的存在性问题的一般思路:
先对结论作出肯定的假设;
然后由肯定假设出发,已知条件或挖掘隐含条件辅以方程思想,数形结合等进行正确的计算、推理,再对得出的结论进行分析检验,判断是否与题设、公理、定理等吻合;
若无矛盾,说明假设正确,由此得出符合条件的数学对象存在;
否则,说明不存在。
存在性问题对学生分析和解决问题的能力提出了较高的要求,有较高的区分度,能较好地体现中考数学的选择功能。
 加载中,请稍侯......
加载中,请稍侯......
精彩评论