行测几何问题中三角形常考考点解题技巧

一、三角形三边长度关系：

两边之和大于第三边，两边之差小于第三边

例1：有若干根长度为3厘米、5厘米、7厘米的木条，用这些木条可以制作可以种不同的三角形?

A.6 B. 8 C. 9 D. 10

【答案】选C

【解析】三角形三边长度关系：两边之和大于第三边，两边之差小于第三边。

分类来数：等边三角形3个，等腰三角形5个，普通三角形1个，一共9个。

二、同底等高三角形面积关系：

同底三角形面积比等于高之比

等高三角形面积比等于底之比

例2：已知三角形ADE 面积为18，三角形CDE面积为12，三角形BCD面积是10，

那么三角形BDE的面积是多少?

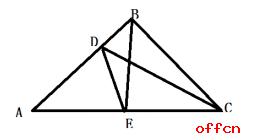
A.8 B.6 C.5 D.3

【答案】:B

【解析】：三角形ADC面积=18+12=30 三角形BCD面积=10 三角形ADC三角形BCD等高，

AD:DB=3：1 三角形BDE=18/3=6

三、相似性

相似比=边长比=周长比

面积比=相似比的平方

例3：如图，DE平行BC，若AD：DB=2:3，那么三角形ADE与三角形ECB面积比是多少?

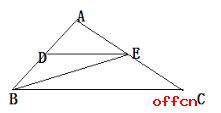
A.1:3 B. 2:5 C. 4:15 D. 5:16

【答案】选C

【解析】三角形ADE与三角形ABC相似，相似比AD：AB=2:5，面积比为4:25，三角形ADE与等高，面积比为2:3,三角形ABC面积25份，则三角形ADE4份，三角形BDE6份，三角形BEC=25-4-6=15份，所求为4:15

四、直角三角形

(1)勾股定理：直角边平方的加和等于斜边的平方

(2)常见直角三角形三边：(3、 4、 5 ) (6、 8、 10 ) (5、 12、 13)

(3)30度60度直角三角形三边比例1：根号3：2

等腰直角三角形三边比例：1:1：根号2

例4：若一直角三角形周长和面积相等，且直角边和为14，三角形面积是多少?

A.20 B. 24 C. 12 D.62

【答案】选B

【解析】题中描述为常见直角三角形，三边为：6、 8、 10 ，面积为(1/2)*6*8=24

对于几何问题考点较多，今天先为大家介绍三角形相关考点，希望同学们通过练习能够有所熟练掌握