“翻译条件法”巧解圆锥曲线大题

cc518学习网精品学习资料总目录

（2015安徽理）

设椭圆E的方程为

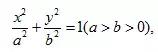
点O为坐标原点，点A的坐标为（a，0），点B的坐标为（0，b），点M在线段AB上，满足|BM|=2|MA|, 直线OM的斜率为

。

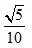
（1）求E的离心率e；

（2）设点C的坐标为（0，-b），N为线段AC的中点，点N关于直线AB的对称点的纵坐标为

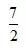
，求E的方程。

分析：

这道题难度不是很大，但是大部分同学没有做出来的原因，不光是这种类型题没有掌握好，还有没有把握好时间，做前面的题目浪费了太多的时间，导致做到这道题时时间不够了，所以得分都不是很高！

同学们在掌握各类题型时，掌握了之后就要多练，能十分钟做完，绝不用十一分钟！

解析：

今天这道题用了“翻译条件”这个方法来解决圆锥曲线问题，也就是说要把题目中晦涩的条件转化为数学式子。

首先，浏览一遍题目，画图（几何题一定要画图）。

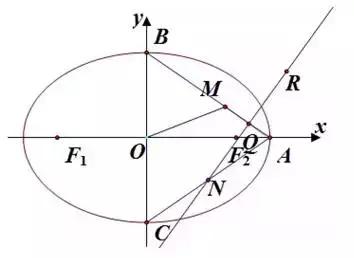
先把已知条件写出来，

能用a,b,c代替也算是已知条件

A(a,0)，B（0,b），

点M在线段AB上，|BM|=2|MA|，

所以得到

，

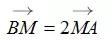
设M(x,y)，根据上面向量关系式得到：

（x,y-b）=2(a-x,-y)，所以得到M点坐标：

,

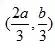
直线OM的斜率为

，

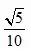
到这里，题目中的条件已经“翻译”完了，接下来要看，这问求什么？

我们发现，求的是离心率，也就是找到a,c的关系。

那么我们先找到a、b的关系

，

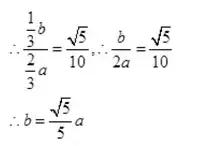
再根据椭圆中的a,b,c的关系即可得到所求，即：

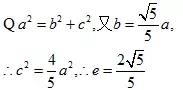
第二问，还是如此的办法：

C（0，-b），

因为N为线段AC的中点，所以N

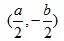
，点N关于直线AB的对称点的纵坐标为

，

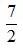
接下来用a，b表示点N的对称点的坐标。

注意：

求对称点的坐标，一般会列两个方程，

点与对称点的连线与已知直线垂直，

所以斜率相乘为-1，点与对称点的中点在已知直线上，

这样列出两个方程来对称点的坐标也就能求出来了！

设点N的对称点为R，坐标为（x,y），直线AB的方程为：

，

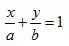
根据上面两点可列方程：

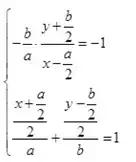
解上面的方程，用a，b表示出y，把a，b的关系带进去，令y=7/2，解得：

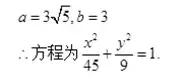
总结：

本题主要考察了椭圆的标准方程及其性质、线段的垂直平分线性质、中点坐标公式、相互垂直的直线斜率之间的关系，考察了推理能力与计算能力，同学们看明白后，一定要自己试试做一遍，有时间的话找类似的题多练习，熟能生巧！