立体几何中的转化关系

使用传统方法解立体几何的问题，主要是充分运用“转化”这种数学思想，最重要的转化是“归面”：将立体几何的问题转化为平面几何的问题。要明确在转化过程中什么变了，什么没变，有什么联系，这是非常关键的。例如：

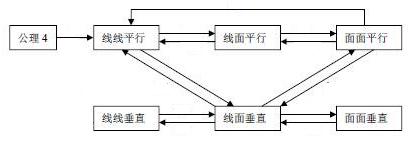
1、平面和平面平行可以转化为线面平行，线面平行又可转化为线线平行。而线线平行又可以由线面平行或面面平行得到，它们之间可以相互转化。同样面面垂直可以转化为线面垂直，进而转化为线线垂直。

2、两条异面直线所成的角转化为两条相交直线的夹角即过空间任意一点引两条异面直线的平行线。

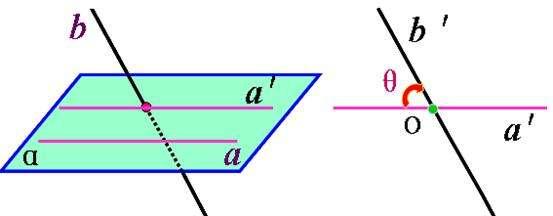
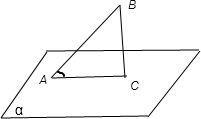
斜线与平面所成的角转化为直线与直线所成的角即斜线与斜线在该平面内的射影所成的角。

3、异面直线的距离可以转化为直线和与它平行的平面间的距离：

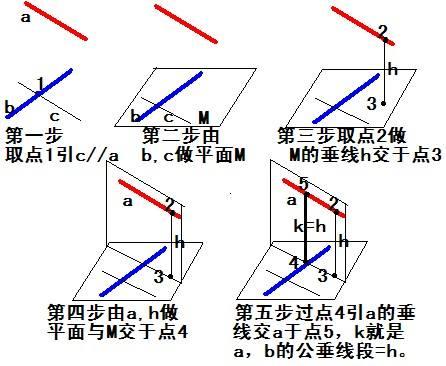
异面直线的距离

也可以转化为两平行平面的距离，即异面直线的距离与线面距离、面面距离三者可以相互转化。而面面距离可以转化为线面距离，再转化为点面距离，点面距离又可转化为点线距离。

说明：在引入空间向量后，角和距离的计算通常采用向量方法。