2021春人教版七年级数学下册章末知识汇总（文件编号：21031405）

2021春人教版七年级数学下册章末知识汇总（文件编号：21031405）

目录：

2021春人教版七年级数学下册章末知识汇总 第5章

2021春人教版七年级数学下册章末知识汇总 第6章

2021春人教版七年级数学下册章末知识汇总 第7章

2021春人教版七年级数学下册章末知识汇总 第8章

2021春人教版七年级数学下册章末知识汇总 第9章

2021春人教版七年级数学下册章末知识汇总 第10章

关注微信公众号：cc518xxzl 可免费领取本资料word完整版！

简介：

类型一　动手操作型问题

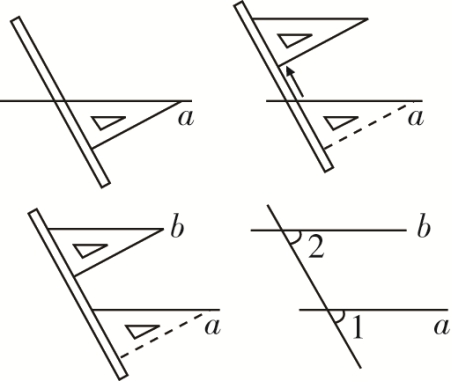
过直线外一点画已知直线的平行线，可按“落、靠、推、画”四字操作：

一落：把三角板一边落在已知直线上；

二靠：紧靠三角板的另一边放一直尺；

三推：把三角板沿直尺的边推到三角板的第一边恰好经过已知点的位置；

四画：沿三角板的第一边画直线，则可画出与已知直线a平行的直线b.

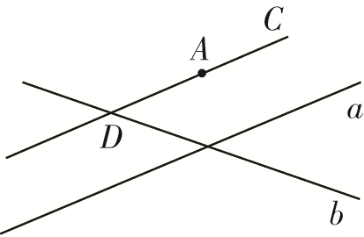
例1　读下列语句，并画出图形．直线a，b是相交直线，点A是直线a，b外的一点，直线CD经过点A且与直线a平行，与直线b相交于点D．

解析：点与直线的位置关系有两种：点在直线上(直线经过点)，点在直线外(直线不经过点)．在同一平面内不重合的两直线的位置关系也是两种：相交和平行．

解：如图所示．

类型二　判定两直线平行的方法

判定两直线平行既是本章重点，又是难点，判定平行的方法有：

1．平行线的定义：在同一平面内，不相交的两条直线叫做平行线；

2．平行公理的推论：如果两条直线都和第三条直线平行，那么这两条直线也平行．即平行于同一条直线的两直线平行；

3．判定定理1：同位角相等，两直线平行；

4．判定定理2：内错角相等，两直线平行；

5．判定定理3：同旁内角互补，两直线平行；

6．命题：“垂直于同一直线的两直线平行”．

判定方法的实质就是通过角度的数量关系“转化”为两直线的位置关系．运用的关键是找准相等或互补的角是由哪两条直线被哪一条直线所截形成的．判定两条直线平行时，第一种方法一般不常用， 第六种不能直接作为定理用，要“转化”为判定公理或判定定理．其他四个方法要灵活使用，证明方法要合理选择．一个题的证法可能有多种思路，我们要善于从中找出最合理的思路和方法．证法的正确书写我们也要仔细模仿，多做多练，逐步掌握．

例2　如图，∠ADE＝∠A, ∠CNM＝∠B．求证：MN∥CD．

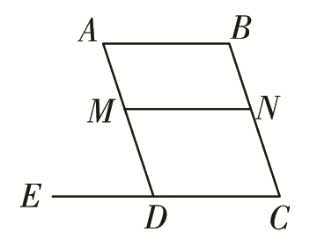
解析：判定MN∥CD的思路有很多．(1)∠NMD＝∠ADE.(2)∠NMD＋∠MDC＝180°.(3)∠AMN＝∠ADC．(4)平行公理的推论等．同时一种思路有可能有多种变式．本题根据题目条件和图形特点，可选择的思路是：由∠A＝∠ADE推出AB∥DC，由∠CNM＝∠B推出AB∥MN，最后根据平行公理的推论得到MN∥CD．

证明：∵∠A＝∠ADE (已知)，

∴AB∥DC (内错角相等，两直线平行)．

又∵∠CNM＝∠B(已知)，

∴AB∥MN(同位角相等，两直线平行)

∴MN∥CD(平行于同一条直线的两条直线平行)．

类型三　巧作辅助线

我们在处理两条平行线间“折线”与“拐角”问题时，通常是在拐点处作平行线，从而构造出一些相等的角或互补角，使得“已知量”和“未知量”之间的等量关系更清晰．

例3　如图所示，已知AB∥CD，∠1＝∠2.试说明∠BEF＝∠EFC．

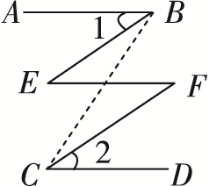
解析：若连接BC，则可以建立起AB与CD之间的关系，同时也可充分利用AB∥CD，∠1＝∠2等条件来解题，所以本题应作辅助线帮助解决问题．

证明：连接BC．

∵AB∥CD，

∴∠ABC＝∠BCD(两直线平行，内错角相等)．

又∵∠1＝∠2，∴∠EBC＝∠FCB．

∴EB∥CF(内错角相等，两直线平行)．

∴∠BEF＝∠EFC(两直线平行，内错角相等)．

类型四　改写命题

把命题的主词连同它的修饰部分，经过重新组织或添加一些词语，写成“如果……”部分，宾词写成“那么……”部分，把它们连接成一个完整的句子，就得到改写成的命题．

例4　用“如果……，那么……”改写命题．

(1)同角的补角相等；

(2)两个无理数的积仍是无理数．

解析：改写命题应先分析命题，明确找到所判断的对象是谁．“如果”后是它满足的条件，“那么”后是它具有的结论．

解：(1)如果两个角是同一个角的补角，那么这两个角相等．

(2)如果两个数是无理数，那么这两个数的积仍是无理数．

类型五　文字型命题的证明及步骤

推理的过程叫做证明，它的一般格式是：从题设出发，经过推理，直到最后得出结论，每步推理都以定义、公理或定理作依据．证明的一般步骤为：

1．审题：分清命题的题设与结论．

2．画图：依照题意画出图形．画图时要做到图形正确且具有一般性，切忌将图形特殊化．

3．写出“已知”、“求证”：按照图形，将题设与结论“翻译”成“已知”、“求证”．

4．探求证题思路：根据已知条件，用学过的定义、公理、定理进行分析、探求：如何证得结论，一步不能证出，能否多步进行．

5．写出证明过程：证明的每一步都要做到叙述清楚，有理有据．

例5　求证：两条平行直线被第三条直线所截，内错角的平分线互相平行．

解析：这个命题可改写为：如果两条直线被第三条直线所截，那么内错角的平分线互相平行．于是可知这个命题的题设是两条直线被第三条直线所截，结论是内错角的平分线互相平行．然后可以画出草图，从而写出已知，求证及证明过程．

解：已知：如图，AB∥CD，EG，FR分别是∠BEF，∠EFC的平分线．

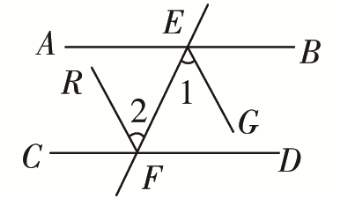
求证：EG∥FR.

证明：∵AB∥CD(已知)，

∴∠BEF＝∠EFC(两直线平行，内错角相等)．

∵EG，FR分别是∠BEF，∠EFC的平分线(已知)，

∴2∠1＝∠BEF，2∠2＝∠EFC(角平分线定义)，

∴2∠1＝2∠2(等式性质)，

∴∠1＝∠2(等式性质)，

∴EG∥FR(内错角相等，两直线平行)．

类型六　巧用平移求面积

运用平移后的图形不改变图形的形状和大小的性质，可巧妙的解决有关求面积的问题．

例6　如图，在长方形ABCD中，横向阴影部分是长方形，另一阴影部分是平行四边形，根据图中标明的数据，其中空白部分的面积是多少？

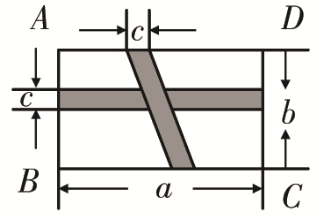
解析：利用“平移不改变图形的形状和大小”这一性质可使本题迅速解决．由图形可知，四个空白四边形经过平移可以组成一个长方形，其长为(a－c)，宽为(b－c)，求出这个新长方形的面积就是空白部分的面积．

解：面积为(a－c)(b－c)＝ab－ac－bc＋c².