直线和圆的位置关系(一)
学习要求
1.理解直线与圆的相交、相切、相离三种位置关系,掌握它们的判定方法.
2.掌握切线的性质和切线的判定,能正确作圆的切线.
课堂学习检测
一、基础知识填空
1.直线与圆在同一平面上做相对运动时,其位置关系有(3种),它们分别是相离、相切、相交.
2.直线和圆有两个公共点时,叫做直线和圆相交,这条直线叫做圆的割线.
直线和圆有一个公共点时,叫做直线和圆相切,这条直线叫做圆的切线.
这个公共点叫做切点.
直线和圆没有公共点时,叫做直线和圆相离.
3.设⊙O的半径为r,圆心O到直线l的距离为d,
_____ d>r ____,直线l和圆O相离;
_____ d=r ____,直线l和圆O相切;
_____ d<r ____,直线l和圆O相交.
4.圆的切线的性质定理是圆的切线垂直于过切点的半径.
5.圆的切线的判定定理是经过半径的外端并且垂直于这条半径的直线是圆的切线
6.已知直线l及其上一点A,则与直线l相切于A点的圆的圆心P在过A点且与直线l垂直的直线上(A点除外)
二、解答题
7.已知:Rt△ABC中,∠C=90°,BC=5cm,AC=12cm,以C点为圆心,作半径为R的圆,求:
(1)当R为何值时,⊙C和直线AB相离?
(2)当R为何值时,⊙C和直线AB相切?
(3)当R为何值时,⊙C和直线AB相交?
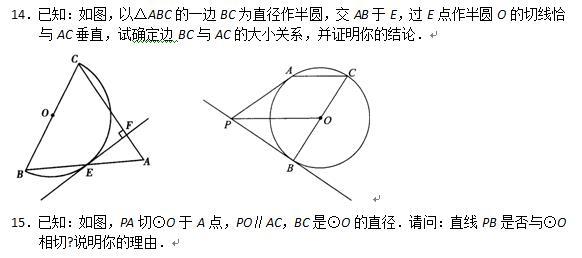
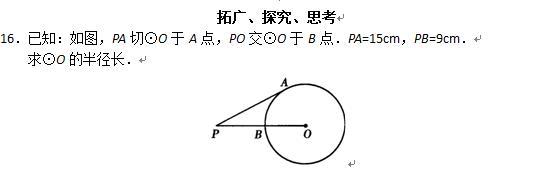
直线和圆的位置关系(二)
学习要求
1.掌握圆的切线的性质及判定定理.
2.理解切线长的概念,掌握由圆外一点引圆的切线的性质.
3.理解三角形的内切圆及内心的概念,会作三角形的内切圆.
课堂学习检测
一、基础知识填空
1.经过圆外一点作圆的切线,这点和切点之间的线段的长.叫做这点到圆的切线长.
2.从圆外一点可以引圆的2条切线,它们的切线长相等.这一点和圆心的连线平分两条切线的夹角.
3.三角形的三个内角的平分线交于一点,这个点到这个三角形的三边的距离相等.
4.与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
5.设等边三角形的内切圆半径为r,外接圆半径为R,边长为a,则r∶R∶a=______.
6.设O为△ABC的内心,若∠A=52°,则∠BOC=____________.
二、解答题
7.已知:如图,从两个同心圆O的大圆上一点A,作大圆的弦AB切小圆于C点,大圆的弦AD切小圆于E点.
求证:(1)AB=AD;(2)DE=BC.
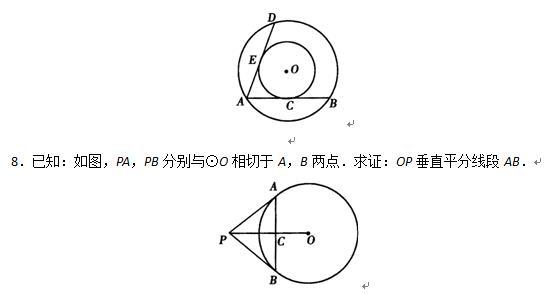
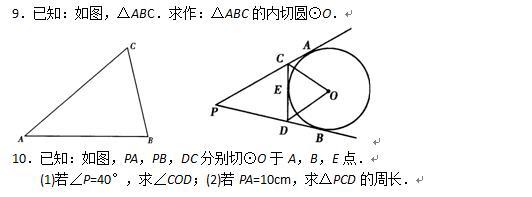
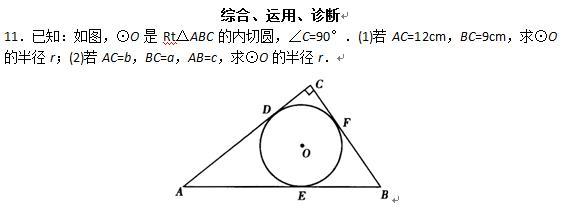
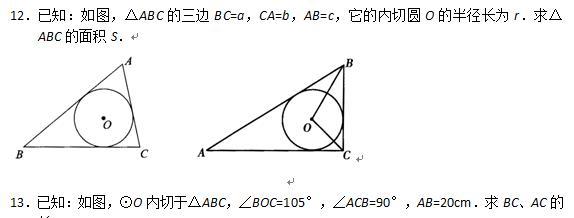
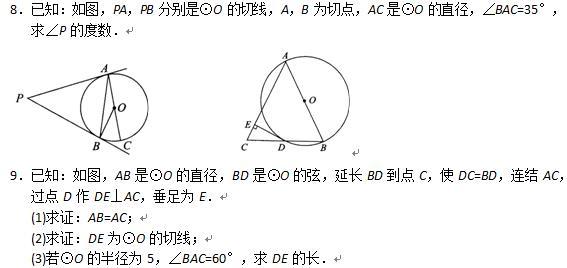
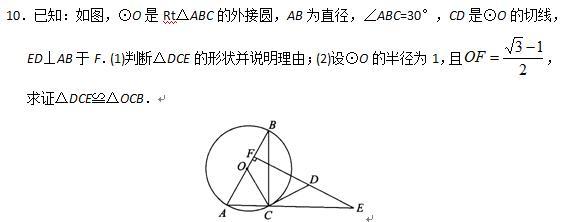
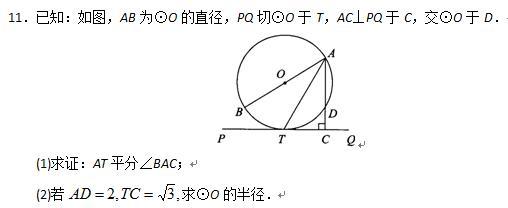
自我检测(二)
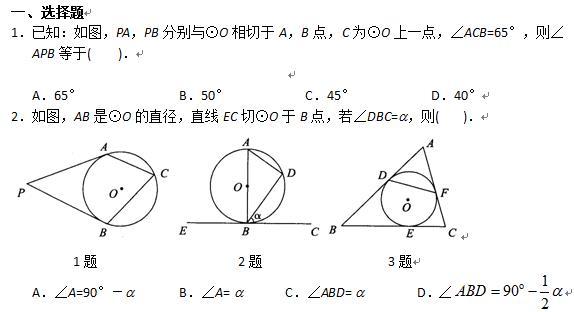

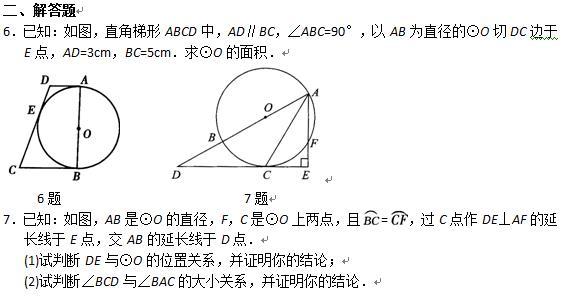
 加载中,请稍侯......
加载中,请稍侯......
精彩评论