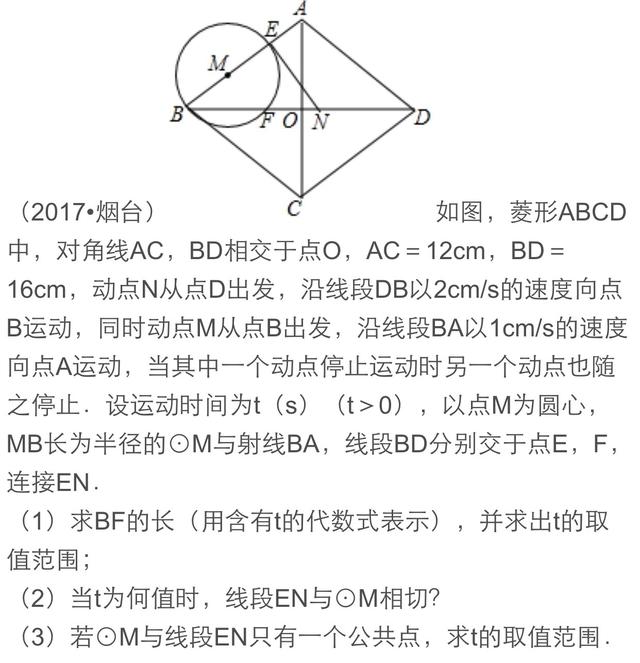
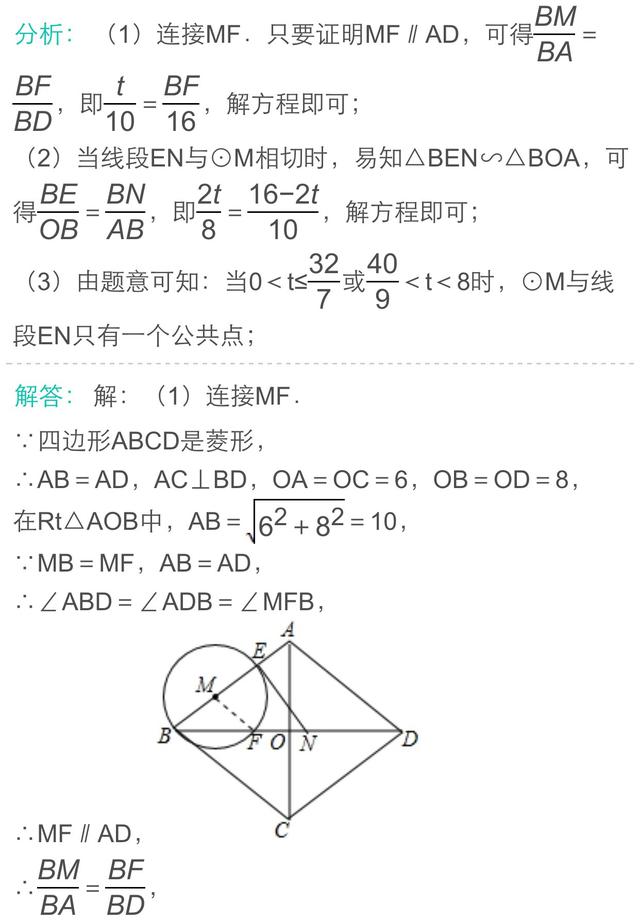
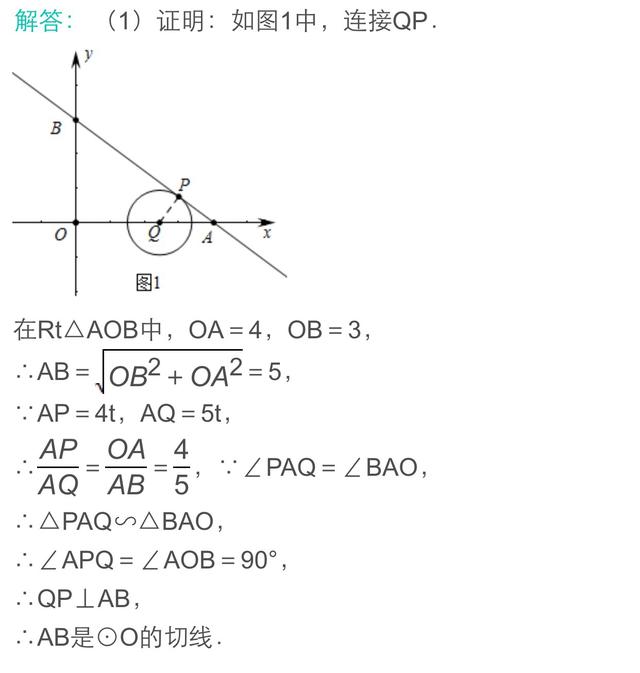
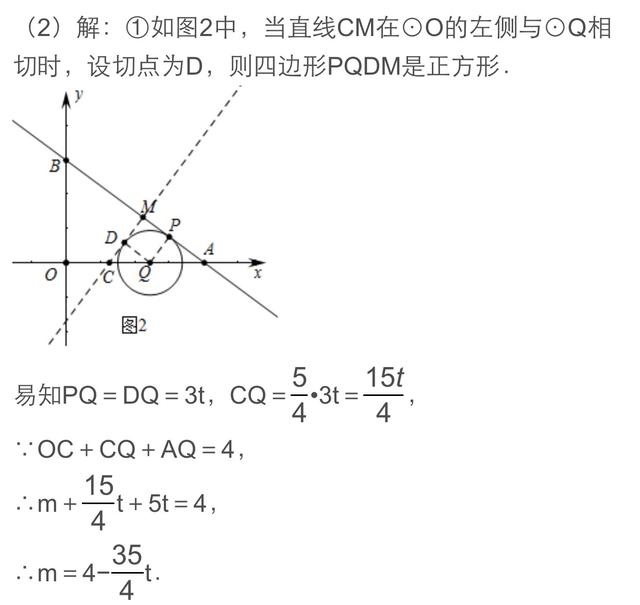
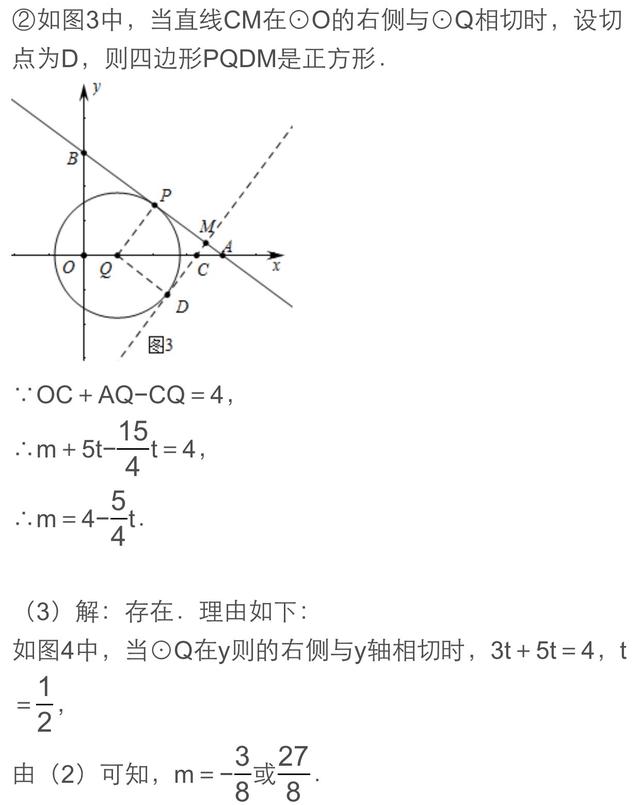
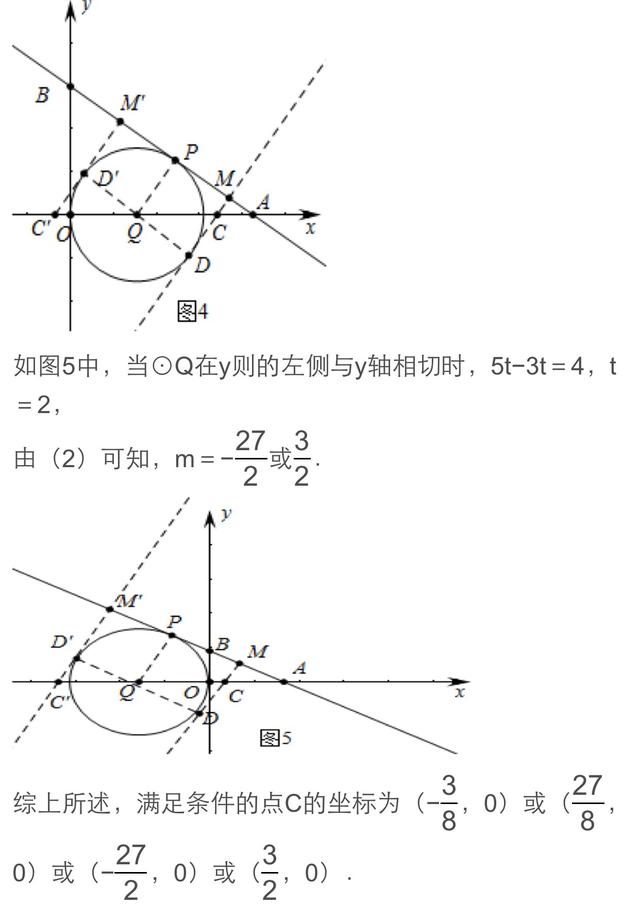
纵观近几年中考数学的区分题，与圆相关的问题大都以圆与直线型图形组成的复合图形为背景,以运动为载体来设计问题，如动态探索性问题，它集代数与几何的众多知识于一体，渗透了分类讨论、转化化归、数形结合、函数方程等重要数学思想,考查综合运用知识分析与解决问题的能力。其中动点与圆问题、动线与动圆问题成为各省市命题的热点。圆与其他章节知识点的联系密切，知识之间相互渗透,相互转化.与圆有关题目题材丰富，背景新颖,具有解法灵活，综合性大,可操作性强的特点，已成为新课程中考的“亮点”。动线与动圆是以线或圆运动为背景进行问题设计的一类动态问题。下面我们以2017年烟台和荆州的两道中考题谈谈这类题目的解法。

中考的“亮点”——《与圆有关的问题》

中考的“亮点”——《与圆有关的问题》

中考的“亮点”——《与圆有关的问题》

中考的“亮点”——《与圆有关的问题》

中考的“亮点”——《与圆有关的问题》

中考的“亮点”——《与圆有关的问题》

中考的“亮点”——《与圆有关的问题》

中考的“亮点”——《与圆有关的问题》

中考的“亮点”——《与圆有关的问题》

中考的“亮点”——《与圆有关的问题》

无论线动还是圆动，都必须抓住图形运动变化过程中“变量”与“不变量”以及它们之间的变化关系。探究几何图形按某种规律运动,必须遵循由简到复杂，由特殊到一般,动静结合，以静制动的辩证法思想。有关线圆动态问题，与直线型知识密切关联，涉及到圆周角定理，垂径定理,直线与圆的位置关系、切线长定理等相关知识。试题的设置往往带有开放性，操作性、探究性和综合性的特点,具有较好的区分度和一定难度，是中考试卷的区分题或压轴题。