第一单元 【大数的认识】

1、 计数单位：一（个）、十、百、千、万、十万、百万、千万、亿等，都是计数单位。

2、 数位：个位、十位、百位、千位、万位、十万位、百万位、千万位、亿位等，都是数位。数位名称就是在相应的计数单位后添一个“位”字，如：万à万位。

3、 数级：个级、万级、亿级……都是数级，一个数级包括四个数位。

数位顺序表：含有数级、数位和相应的计数单位的表格叫数位顺序表，如下。

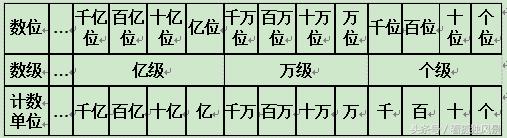
数位顺序表

4、 进率：相邻两个计数单位之间的进率是“十”。

10个一万是十万，10个十万是一百万，10个一百万是一千万，10个一千万是一亿。

5、 数字表示：某个数位上的数字表示几个这个数位的计数单位。

如：12367 中的2在千位上，表示 “2个千”

某个数级上的数字表示几个这个数级的计数单位。

如：36472845中的3647在万级上，表示 “3647个万”

大数的读法：从高位读起，一级一级往下读，每级读完后加上该级的计数单位。每一级末尾的0不读，中间连续有几个0都只读一个0。

6、 大数的写法：按照数级从高到低写数，当哪一位上一个计数单位也没有，就在哪一位上写0。

7、 读写数检验方法：读数和写数可以互相检验，即读数后再写出来和原数比对，而写数后可以自己读出。

8、 比较亿以内数的大小：大数的比较方法和以前相同，先把数位对齐，位数多的数大；位数一样的，从最高位的数字依次往右比起。

9、 四舍五入法：求“近似数”的一种方法，首先确定需要精确到的数位，将其后面的数作为“尾数”，对尾数最高位上的数字进行取舍。0~4为“舍”，尾数清零且精确数位的数字不变，5~9为“入”，尾数清零且精确数位上的数字加1。

注意：四舍五入后的结果是近似数，所以符号一定要用“≈”！

10、 改写成不同计数单位的数：

（1）整万、整亿的数：将个级的4个0改写成“万”，将万级、个级共8个0改写成“亿”

注意：整万、整亿的数的改写属于准确数，要用“=”连接！

（2）非整万的数改写成以“万”为单位的数：将万位以后的数作为尾数，对尾数的最高位（千位）四舍五入，再改写成以“万”为单位的数

（3）非整亿的数改写成以“亿”为单位的数：将亿位以后的数作为尾数，对尾数的最高位（千万位）四舍五入，再改写成以“亿”为单位的数

11、十进制：每相邻两个计数单位之间的进率之间都是十的计数方法叫做十进制计数法。

12、自然数：表示物体个数的1，2，3，4，5，6，7，8，9，10，11，……都是自然数。一个物体也没有，用0表示，0也是自然数。最小的自然数是0，没有最大的自然数，自然数的个数是无限的。

13、计算工具的认识：

（1）算盘：发明算盘的是中国。算盘有上下两档，上档每颗珠子代表5，下档每颗珠子代表1，每根杆相当于一个数位，如“万位上的一颗上珠”表示“5个万”。

（2）计算器：CE是“清除键”，ON/C是“开关及清屏键”。

第二单元 【公顷与平方千米】

1平方米=100平方分米 1平方分米=100平方厘米

平方米——平方分米——平方厘米 相邻两个面积单位之间的进率是100

1公顷=10000平方米 1平方千米=100公顷=1000000平方米

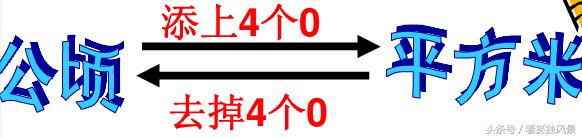
小化大，减0；大化小，加0

公顷做单位的比如：土地、花园、公园、厂区、森林、广场；

平方千米做单位的比如：国土面积、省或城市面积、耕地面积、陆地面积。

第三单元 【角的度量】

1、 线段：是直线的一部分，具有2个端点，可以度量长度，不可延长。

2、 射线：是直线的一部分，只有1个端点，可以向一端无限延长，不可度量。

3、 直线：没有端点（或者说“有0个端点”），可以向两端无限延长，不可度量。

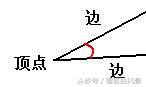
4、 角：从一点引出两条射线所组成的图形叫做角。这一点叫做角的“顶点”，两条射线叫做角的两条“边”。角要用弧线表示大小。

5、 过点画直线的数量：

过一点可以画无数条射线、无数条直线。

因为“两点可以确定一条直线”，所以过两点只能画出一条直线。

6、 角的度量方法：量角的大小，要用量角器。

角的计量单位是“度”，用符号“°”表示。把半圆分成180等份，每一份所对的角的大小是1度，记作1°。

步骤：（1）量角器的中心与角的顶点重合

（2）（量角器的其中一条）0刻度线与角的一条边重合

（3）角的另一条边所对应的（与0刻度线同圈的）刻度就是这个角的度数

7、 角的大小比较：角的大小与角的两边长短没有关系。角的大小要看两条边张开的大小，张开得越大，角越大。

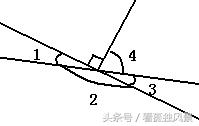
8、 会求一个已知角的余角、补角和对顶角：

如右图，若∠3=25°，则∠4=90°－25°=65°，若∠1=25°，则∠2=180°－25°=155°，若∠1=25°，则∠3=∠1=25°

9、角的分类：

（1） 锐角＜90°， 直角=90°，90°＜钝角＜180°，

平角=180°，1平角=2直角，1周角=360°=2平角=4平角

10、 角的绘制方法：

A、用量角器画角（如画65°的角）

（1）画一条射线，作为角的顶点和一条边

（2）使量角器的中心和射线的端点重合，0刻度线和射线重合

（3）在量角器（与0刻度线同圈的）65°刻度线的地方点一个点

（4）以画出的射线的端点为端点，通过刚画的点，再画一条射线（因为“两点确定一条直线”，用端点和刚画的点来确定另外一条边的位置）

（5）画小弧线，标注角的度数。

B、用三角板画角（如画75°的角）

画角方法和用量角器的相同，只是标注方法不同，需要标出这个角是由哪几个三角板上的角组合（加或减）而成的。

注：用三角板可画出所有15°倍数的角，如75°、105°、120°、135°、150°和165°

而用“一副（两个）三角板”可以“拼出”75°、105°、120°、135°、150°这几个角

11、 图形计数：

数线段：2+3+……端点个数

数射线：端点个数×2

数角：2+3+……+射线条数

第四单元 【三位数乘两位数】

1、 两位数乘一位数的口算乘法：（如16×3）把16分成10和6，先算10×3＝30，再6×3＝18，最后算30＋18＝48，所以16×3＝48。

2、 三位数（末尾有0）乘一位数的口算乘法：（如160×3）把末尾0的部分先不看，看成16×3，口算出得48，再在得数的末尾添上所有去掉的0，160末尾有1个0，所以添上1个0得480，所以160×3＝480。

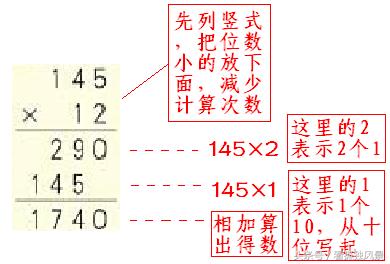
3、 笔算乘法的方法：

先用两位数个位上的数去乘三位数，得数的末位与两位数的个位对齐；再用两位数十位上的数去乘三位数，得数的末位与两位数的十位对齐；最后把两次结果加起来。如145×12。

4、 末尾有0的笔算乘法：如160×30=

（1） 先将末尾的0的部分和“非0”部分分别对齐

（2） 用虚线隔开，虚线要往下延长到得数的地方

（3） 把“非0”部分按照原来的方法算出得数

（4） 把末尾的0的部分的0添在得数末尾，一共有几个0就添几个0。

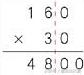
5、 速度关系及“复合单位表示法”：

每小时行60千米 也可以说成是 速度为60千米/时

每分钟行225米 也可以说成是 速度为225米/分

关系式： 速度 × 时间 ＝ 路程

所以 速度 ＝ 路程 ÷ 时间

时间 ＝ 路程 ÷ 速度

做应用题时应特别注意速度的单位，例如：王叔叔从县城出发去120千米外的王庄乡送化肥，用了2小时，问平均每小时行多少千米？

问题是“平均每小时行多少千米？”问的是速度，所以要知道路程和时间。

120 ÷ 2 ＝ 60 （千米/时） 求的是速度，单位也要是速度！

6、 验算的方法：乘法验算用交换因数，但要注意步骤可能会变多，步骤数量取决于下面的因数有几个“非0”的数字

7、 “买N送一”问题的解决：

例：每棵树苗16元，买3棵送1棵。一次买3棵，每棵便宜多少钱？

解决方法1：先算实际付的钱数： 16×3=48（元）

再算实际得到的棵数： 3＋1=4（棵）

接着算平均每棵实际付的钱数： 48÷4=12（元）

最后算每棵便宜的钱数： 16－12=4（元）

解决方法2：先算总共便宜的钱数： 16×1=16（元）

再算总共得到的棵数： 3＋1=4（棵）

最后算每棵平均便宜多少钱： 16÷4=4（元）

8、 “够不够”问题的解决：

例1：一个计算器24元，李老师要买4个。他带了100元，钱够吗？ P48

计算过程除了应该算出共需多少钱 24×4=96（元） 之外，还应当与带来的钱数进行比较，即 100＞96 ，不用带单位但要注意同样单位的才能比较。

例2：小军家距离学校420米，小军上学时平均每分钟走62米，6分钟内他能走到学校吗？

这题一看62不是整十数，当然不会去用除法啦，用我们学过的乘法最简单：

解：62×6=372（米） 372＜420 答：6分钟内他不能走到学校。

9、 积的变化规律：

两个数相乘，其中一个因数不变，另一个因数乘（或除以）几（0除外），积也乘（或除以）几。

两个数相乘，其中一个因数乘几（0除外），另一个因数除以几（0除外），积不变。

10、 乘法估算：

一要注意要符合实际情况，接近准确值。

二是要将其中一个因数或两个因数“四舍五入”成相近的整十、整百数，简化计算。

第五单元 【平行四边形和梯形】

1、 同一平面内两条直线的位置关系：

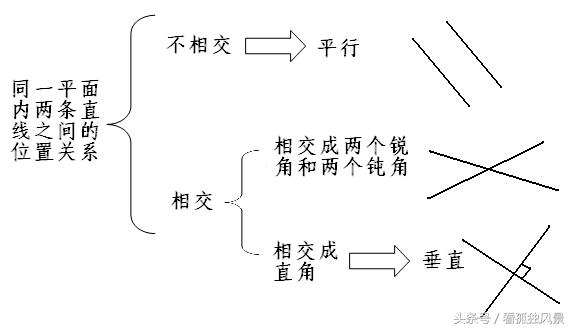
2、 平行：在同一个平面内不相交的两条直线叫做平行线，也可以说这两条直线互相平行。 P

3、 垂直：如果两条直线相交成直角，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，这两条直线的交点叫做垂足。

4、 画垂线和平行线的方法：靠、移、画、验 （一定要看书、操作一下！）

5、 点到直线的距离：从直线外一点到这条直线所画的垂直线段最短，它的长度叫做这点到直线的距离。 注意：缩句后变成——垂直线段 的 长度 叫 距离。

6、 平行线的性质：两条平行线之间的距离处处相等。

这个性质可以用来证明长方形对边相等且平行。

7、 画长方形和正方形时的要点：用垂直和平行的方法画图，注意标注：长方形要标出一组邻边的长度，正方形要标出一条边的长度（如果有的话），再标上直角（3个及以上）或者在旁边写出“长方形”、“正方形”。

8、 平行四边形和梯形：两组对边分别平行的四边形叫做平行四边形；只有一组对边平行的四边形叫做梯形。

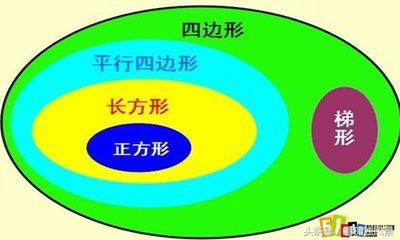
9、 集合图：用集合图来表示图形之间的关系

10、平行四边形的特性：四边形具有“容易变形”的特性，或叫做“不稳定性”。

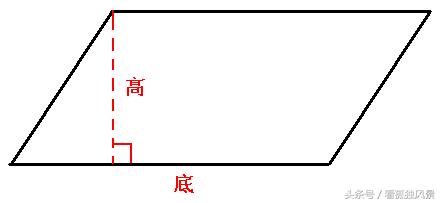
11、底和高：从平行四边形一条边上的一点到对边引一条垂线，这点和垂足之间的线段叫做平行四边形的高，垂足所在的边叫做平行四边形的底。

从梯形上底上的一点到下底引一条垂线，这点和垂足之间的线段叫做梯形的高，梯形的底是固定的两条边——上底和下底。

10、 特殊的梯形：两腰相等的梯形叫做等腰梯形，只有一条腰和上、下底垂直的梯形叫做直角梯形。等腰梯形不可能是直角梯形，直角梯形也不可能是等腰梯形。

替换高清大图

11、 四边形内角和：四边形的内角和都是360°。

12、 图形的拼组（请自己画画看）：

（1） 两个完全一样的三角形可以拼成一个平行四边形。

（2） 两个完全一样的平行四边形可以拼成一个平行四边形。

（3） 两个完全一样的长方形可以拼成一个长方形。

（4） 两个完全一样的正方形可以拼成一个长方形。

（5） 两个完全一样的梯形可以拼成一个平行四边形。

（6） 两个完全一样的直角梯形可以拼成一个长方形或平行四边形。

第六单元 【除数是两位数的除法】

1、 除法的意义：除法表示从总数中连续减去相同的数。在以下4种情况的时候需要用到除法：

（1）求总数中含有几个每份的量，如 求180里有几个30——》180÷30

（2）求从总数中能连续减去几次每份的量，如 求46连续减去几个2后为0——》46÷2

（3）求一个数是另一个数的几倍，如 求160是40的几倍——》160÷40

（4）求将总数平均分成几份，如 求把240平均分成6份，每份是多少——》240÷6

其中，（1）（2）（3）类似，都是求“包含”的关系。

2、 除法中的数量关系（非常重要！）：

被除数÷除数＝商……余数 被除数＝除数×商＋余数

除数＝（被除数－余数）÷商 商＝（被除数－余数）÷除数

余数＝被除数－除数×商

3、 两位数除以两位数（末尾都有0）的口算乘法：（如160÷20）把160和20末尾的0各去掉一个，相当于算16÷2，记作160÷20＝8。 理由见“商不变规律”

4、 “除以”和“除”的不同： 读法、意思有不同，常作为考点

5、 除数是两位数的笔算除法的方法：

从被除数的高位除起，先用除数试除被除数的前两位，如果它比除数小，再试被除数的前三位；除到被除数的哪一位，就把商写在那一位上面；每次除后余下的数必须比除数小。

最后根据竖式补充完横式，注意要写余数。

6、 直接判断商是几位数的方法：

三位数除以两位数，比较被除数的前两位与除数的大小，除数大商就是一位数，除数小商就是两位数。

典型考题：□38÷53，要使商是一位数/两位数，□可以填几？

7、 商的变化规律：

（1） 在除法算式中，被除数不变，除数乘以（或除以）几（0除外），商反而要除以（或乘以）相同的数。

（2） 在除法算式中，除数不变，被除数乘以（或除以）几（0除外），商也要乘以（或除以）相同的数。

（3） 在除法算式中，被除数和除数同时乘以（或除以）相同的数（0除外），商不变。这叫做“商不变规律”（或商不变性质）。

简便记法：“被除数不变时，除数和商是反向变化的，其余都是同向变化的”

8、 运用商不变规律简化竖式：

当被除数和除数末尾都有0时，可以运用商不变规律简化竖式，在被除数和除数末尾划掉相同个数的0，按照划掉0后的竖式进行计算，得出的余数如果不是0，还要再添上0，原来各去掉几个就添上几个

9、 估算的方法：

先将除数看成近似的整十数，再将被除数看成除数估成的整十数的倍数，以此估算出商。如下图

10、 笔算除法验算的方法：

笔算除法的验算一定要用乘法，不可用除法验算！

用除数与商相乘，再加上余数，看是否等于被除数。

11、 解决问题应当注意的要点：

（1）常考的数量关系

单价×数量＝总价 速度×时间＝路程 工作效率×工作时间＝工作总量

单价＝总价÷数量 速度＝路程÷时间 （注意速度单位！） 效率＝工作量÷时间

其中速度单位是常考点，如：

叔叔开车从A地送货到B地，去时每小时行60千米，用了5小时，回来时少用了2小时，回来时的平均速度是多少？

解决方法：①求回来的平均速度，速度＝路程÷时间

先算出两地路程，也就是去时的路程，同时也是回来时的路程 60×5＝300（千米）

再算出回来时的时间 5－2＝3（小时）

最后算出回来时的速度，注意速度单位 300÷3＝100（千米/时）

（2）倍数问题的技巧

例题：4箱蜜蜂一年可以酿300千克蜂蜜。小林家养了这样的蜜蜂12箱，一年可以酿多少千克蜂蜜？

解法一： 可以先算出每一箱蜜蜂一年可以酿多少蜂蜜（即求出1倍的量300÷4＝75（千克）

再算12箱蜜蜂一年可以酿多少蜂蜜 75×12＝900（千克）

解法二： 也可以算12箱是4箱的几倍 12÷4＝3 倍数作为单位不用写出来

再算出同样时间内蜜蜂能酿出的蜂蜜 300×3＝900（千克）

（3）最优方案（用同样的钱买最多的商品） 课本93页第9题

解决方法： 先看哪种方案更优，尽量使用这种方案来买，最后如果有剩余再考虑其他方案

例题： 商场卖衬衫，一件29元，两件49元，老师有185元，最多可以买多少件？还剩几元？

解决方法：比较两种方案，“两件49元”的更便宜（一件只要不到25元），所以先尽量用“两件49”的方法买，可以买3套（共6件），算式为185÷49＝3（套）……38（元），2×3＝6（件），发现最后的余数还可以买一件29元的，38－29＝9（元），6＋1＝7（件）。所以最后可以买到7件，剩余9元。

第七单元 【统计】

1、 画统计图的原则：“图表合一”，即统计表中有的项目、数值、单位、名称都应该在统计图中反映出来，而且应该一一对应，不得私自改变。

2、 条形统计图的六要素：标题、横轴、纵轴、条形、数值、图例。

3、学会统计图中提取信息，发现问题，进行合理的判断、预测和决策，并能解决生活中的简单问题。

第八单元 【数学广角】

1、 烙饼问题的解决：

在每次只能烙两张饼，两面都要烙的情况下：

①烙3张饼：先烙1，2号饼的正面，接着烙1号饼的反面和3号饼的正面，最后烙2，3号饼的反面。

②烙多张饼：如果要烙的饼的张数是双数，2张2张的烙就可以了，如果要烙的饼的张数是单数，可以先2个2个的烙，最后3张饼按上面的最优方法烙，最节省时间。

一般的解决方法：

公式： 烙饼总时间＝每次烙的时间×[（2×烙饼总数）÷每次烙的饼数]

如每次可以同时烙3张饼，每次要烙5分钟，要烙9张饼的时间是5×[（2×9）÷3]＝30（分）

问题本质： 烙饼问题其实是统筹方法的一个分支，其实质是利用好烙锅的容量空间，使每次烙的效率最高。

2、 统筹安排时间问题：

原则有两个：其一，“分清先后”——找出事物发生的必然先后顺序；其二，“同时进行”——在做不需要人照看的事的同时做其他事，这样就可以节约时间。

3、田忌赛马（对策论）：田忌用下等马对齐王的上等马，用上等马对齐王的中等马，用中等马对齐王的下等马。三场两胜，田忌胜出。