第一单元小数乘法

1、小数乘整数：意义——求几个相同加数的和的简便运算。

如：1.5×3表示1.5的3倍是多少或3个1.5是多少。

计算方法：先把小数扩大成整数；按整数乘法的法则算出积；再看因数中一共有几位小数，就从积的右边起数出几位点上小数点。

2、小数乘小数：意义——就是求这个数的几分之几是多少。

如：1.5×0.8（整数部分是0）就是求1.5的十分之八是多少。

1.5×1.8（整数部分不是0）就是求1.5的1.8倍是多少。

3、小数乘法的计算方法：先按整数乘法算出积、在数出因数中一共有几位小数，点上小数点，位数不够添上0。小数末尾的0要去掉。例如： 4.25×0.108=

（1）、一个数（0除外）乘以小于1的数，积比这个数小。

如：3.2×0.88﹤3.2 0.13×4.76﹤4.76

（2）一个数（0除外）乘以大于1的数，积比这个数大。

如：0.23×1.04﹥0.23 3.5×7.3﹥7.3

4、求近似数的方法一般有三种：

⑴四舍五入法；⑵进一法；⑶去尾法

5、小数四则运算顺序跟整数是一样的。先乘除，后加减，有括号先算小括号。

6、运算定律和性质：

加法：加法交换律：a+b=b+a 加法结合律:(a+b)+c=a+(b+c)

※一个数连续的减去几个数，可以把后面的所有减数相加，再和倍减数相减：a –b-c=a-(b+c)

乘法：乘法交换律：a×b=b×a

乘法结合律：(a×b)×c=a×(b×c)见2.5找4或0.4，见1.25找8或0.8

乘法分配律：(a+b)×c=a×c+b×c或a×c+b×c=(a+b)×c（b=1时，省略b）

变式： (a-b)×c=a×c-b×c或a×c-b×c=(a-b)×c

练习：

下列各题怎样简便就怎样算。

0.78×101 6.4×2.8+2.8×3.6 0.25×1.25×4×8

0.125×3.2×2.5 0.8×2.6×125 32×0.25

（0.25+2.5）×40 8.8×0.125 86.7-13.6-26.4

4.4×25 17.17-6.8-3.2-6.17 17.45-（3.2+12.45）

第二单元 位置

1、确定物体的位置，要用到数对（先列：即竖，后行即横排）。用数对要能解决两个问题：一是给出一对数对，要能在坐标途中标出物体所在位置的点。二是给出坐标中的一个点，要能用数对表示。

练习：1、请你在右面的方格图里描出下列各点,并把这几个点顺次连接成一个封闭图形,你能发现什么?

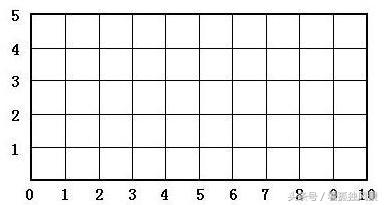
A（2,1） B（7,1） C（4,4） D（9,4）

第三单元小数除法

1、小数除法的计算方法：先把除数扩大成整数。除数扩大多少倍，被除数也只能扩大多少倍，商的小数点和被除数的小数点对齐。不够除时商0。除到最后仍然有余数要添0往下出。 例如： 50.4÷0.28=

（1）、一个数（0除外）除以大于0的数，商比原来的数小。

例如：4.25÷1.01﹤4.25

（2）、一个数（0除外）除以大于0且小于1的数，商比原来的数大。

例如：0.99÷0.99﹥0.99

2、、在实际应用中，小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数，求出商的近似数。

3、除法中的变化规律：①商不变性质：被除数和除数同时扩大或缩小相同的倍数（0除外），商不变。②除数不变，被除数扩大（缩小），商随着扩大（缩小）。③被除数不变，除数缩小，商反而扩大；被除数不变，除数扩大，商反而缩小。

4、循环小数：一个数的小数部分，从某一位起，一个数字或者几个数字依次不断重复出现，这样的小数叫做循环小数。 循环节：一个循环小数的小数部分，依次不断重复出现的数字。如6.3232……的循环节是32.简写作6.32

5、小数部分的位数是有限的小数，叫做有限小数。小数部分的位数是无限的小数，叫做无限小数。小数分为有限小数和无限小数。

练习:

1、一个两位小数保留一位小数后是1.5，这个两位小数最大是(　　)，最小是(　　).

2、把3.8米长的铁丝平均截成5端,每段长（ ）米,还剩（ ）米

3、 两个数相除的商是0.39，如果被除数扩大10倍，除数也扩大10倍，那么商是(　　).

4、用竖式计算，商是循环小数的用简便写法表示出来.

15.2÷4　　　 　25.84÷1.7　　　 　47.04÷1.4 0.196÷0.56　　 　

第四单元可能性

1、事件发生有三种情况：可能发生、不可能发生、一定发生。

2、可能发生的事件，可能性大小。把几种可能的情况的份数相加做分母，单一的这种可能性做分子，就可求出相应事件发生可能性大小。

练习：

1、口袋里只有10个白色围棋，任意摸出一个，肯定是（　　）色的。

2、盒子里有9个红色跳棋子，2个黄色跳棋子，任意摸出一个，可能出现（　　）种情况，分别是（　　 ）和（　　 ），摸出（　　）色跳棋子的可能性大。

3、计算下面各题，怎样简便就怎样计算。

4.05÷0.5+10.75 70.3－17.48÷7.6

第五单元简易方程

1、在含有字母的式子里，字母中间的乘号可以记作“·”，也可以省略不写。加号、减号除号以及数与数之间的乘号不能省略。

2、a×a可以写作a·a或a ，a 读作a的平方 2a表示a+a。特别地1a=a这里的：“1“我们不写

3、方程：含有未知数的等式称为方程（★方程必须满足的条件：必须是等式 必须有未知数两者缺一不可）。使方程左右两边相等的未知数的值，叫做方程的解。求方程的解的过程叫做解方程。※所有的方程都是等式，但等式不一定都是等式。

4、解方程原理：天平平衡。 等式左右两边同时加、减、乘、除相同的数（0除外），等式依然成立。※方程的解是一个数； 解方程式一个计算过程。=方程右边 所以，X=…是方程的解。※方程的检验过程：方程左边=……

5、10个数量关系式：

加法：和=加数+加数 一个加数=和-另一个加数

例如：x+120=176 58+x=90

减法：差=被减数-减数 被减数=差+减数 减数=被减数-差

例如： x－3.3=8.9 73.2－x=52.5

乘法：积=因数×因数 一个因数=积÷另一个因数

例如：x×4.5=90 6.2x=124

除法：商=被除数÷除数 被除数=商×除数 除数=被除数÷商

例如：x÷78=10.5 8.8÷x=4.4

带括号的方程（先将小括号内的式子看作一个整体来计算，然后再来求方程的解）

例如：3×(x－4)=46 　 　　(８+2x) ÷2=16

含有两个未知数的，我们可以用乘法分配律来解答，求出方程的解。

例如：12x+8x=40 1.3x+x=26

6、实际问题与方程：

行程问题： 路程=速度×时间 速度=路程÷时间 时间=路程÷速度

例如：两辆汽车同时相背而行，4.5小时后两车相距54千米，甲车每小时行32千米，乙车每小时行都少千米？

练习：

1、甲乙两人从相距50千米的地方相向而行，甲每小时行6千米，乙每小时行4千米，当两人之间的距离是10千米时，他们走了多少小时？

2、两列对开的火车在途中相遇，甲车上的乘客看到乙车从旁边开过去，共用了6秒钟，已知甲车每小时行45千米，乙车每小时行36千米，则乙车全长多少米？

2、价格问题：总价=单价×数量 单价=总价÷数量 数量=总价÷单价

例如：小敏买了两套丛书，两套丛书的本数相同。科学丛书每本2.5元，发明家丛书每本3元，共花了22元。每套丛书有多少本？

3、工程问题：工作总量=工作效率×工作时间 工作效率=工作总量÷工作时间

工作时间=工作总量÷工作效率

（1）、农田里二台播种机6小时可以播种2.4公顷，照这样计算3.56小时3台播种机可以播种多少公顷？

（2）李村修一条水渠，计划每天修80米，而实际只用25天完成，比原计划提前5天，实际每天修多少米？（用算术法和方程解）

5、倍数问题：像这类的应用题在几倍前都会有一个“的”“比”字，如果“的”“比”字前得这个量就是问题，我们就可以根据数量关系设这个量为X.列出方程。

例如：(1)、某钢厂有职工1800人，其中男职工是女职工的2.6倍，这个钢厂男、女职工各有多少人？

（2）学校图书馆购进故事书720本书，比科技书的3倍少48本，购进科技书多少本？

第六单元多边形的面积

1、公式：

2、组合图形面积计算：必须转化成已学的简单图形。

练习：

1、平行四边形的面积是48平方分米，底是12分米，高是（　　　 ）.

2．一个平行四边形的面积是9平方分米，底扩大4倍，高不变，它的面积是（ ）平方分米。

3、一个梯形的上底是3米，下底2米，高2米，这个梯形的面积是（　　　 ）平方米

4、一个三角形的面积是4.5平方分米，底是5分米，高是（ ）分米。

5、求下列图形阴影部分的面积。单位：厘米

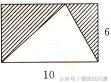
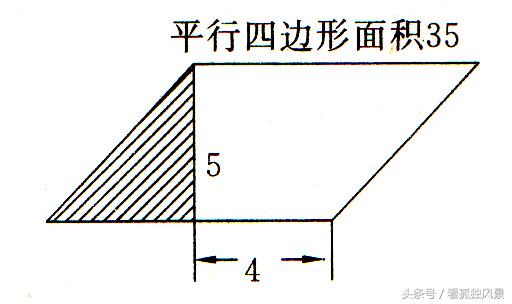
6.、计算下列组合图形的面积

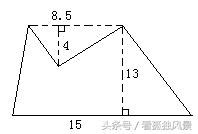
第七单元数学广角——植树问题、鸡兔同笼问题

1、不封闭栽树问题：

（1）一条路的一边两端都栽树=路长÷间隔+1；

已知间隔数，树的棵树，求路长。路长=间隔数×（树的棵树-1）

（2）一条路的一边两端不栽树=路长÷间隔-1

（3）一条路的两边两端都栽树=（路长÷间隔+1）×2

（4）一条路的两边两端不栽树=（路长÷间隔-1）×2

（5）锯木头时间问题：锯一段木头时间=总时间÷（段数-1）

2、封闭图形四周栽树问题：栽树棵树=周长÷间隔

练习：

1、园林工人沿一段长210米的公路一侧植树，一共种了36棵（两端要种）．每两探树之间的距离是多少？

2、一张桌子坐8人，两张桌子并起来坐12人，三张桌子并起来坐16人……照这样计算，六张桌子并成一排可以坐多少人？如果一共有40人，需要多少张桌子并成一排才能坐下？