解题的思路总是多种多样,但是无非是几种方向,要嘛从条件出发,要嘛从结论回溯,实在不行就综合加分析,首尾碰撞一起。
【典型问题】
已知P为正方形ABCD的边BC上一点,AE评分∠DAP交DC于E,求证:DE=AP-BP.
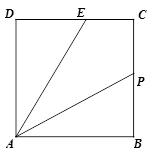
【分析】本题的重要条件是角平分线,其次结论是线段和差的问题,因此都可以有比较好的辅助线添加方法,本题方法多样,下面列举几种,欢迎大家讨论,继续提供更多样的解法,期待您的参与
【解题过程】
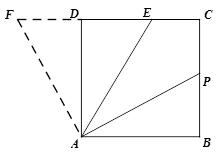
证法一:延长CD到F,使得DF=BP,并连接AF,
易证△ADF≌△ABP,
易得∠FAE=∠FAD+∠DAE=∠PAB+∠PAE=∠BAE=∠FEA,
得FA=FE,
所以AP=AF=FE=DF+DE=BP+DE,所以DE=AP-BP
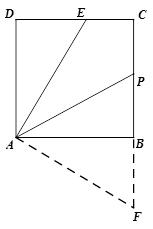
证法二:延长CB到F,使得BF=DE,并连接AF,
易证△ADE≌△ABF,再证∠PAF=∠F=90°-∠BAF,
得AP=PF,即可得到AP=PF=BF+ BP= BP +DE,
所以DE=AP-BP
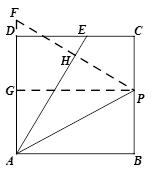
证法三:延长AD到F使得AF=AP,
过点P作PG∥AB交AD于点G,
连接PF交AE于点H
易得PF⊥AE,得∠F=∠AED,
再证明△ADE≌△PGF,
可得AP=AF=AG+GF=BP+DE,
所以DE=AP-BP
还有哪些方法呢?
 加载中,请稍侯......
加载中,请稍侯......
精彩评论