中考数学压轴题讲解分析：一次函数与几何综合问题

下面我们先来看一道典型例题。

中考数学，一次函数与几何相关综合题，典型例题分析1：

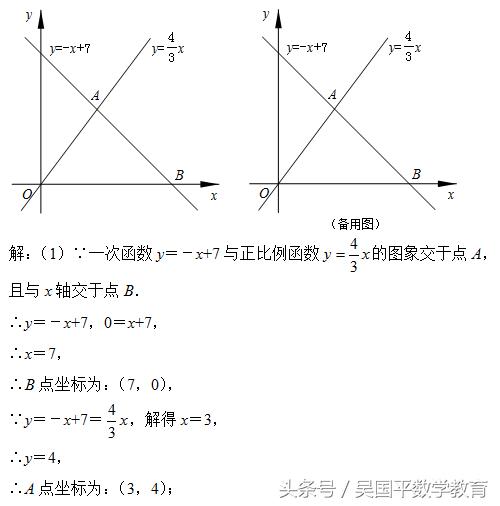
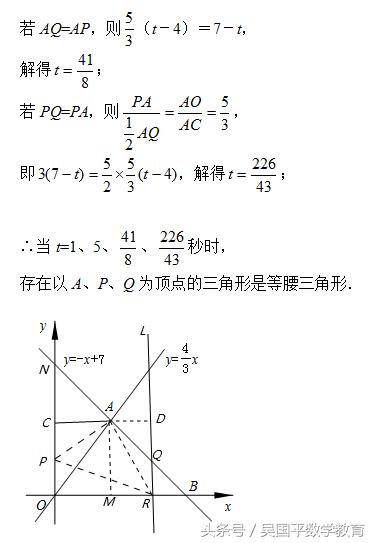
如图，已知一次函数y=－x+7与正比例函数y=4x/3的图象交于点A，且与x轴交于点B．

（1）求点A和点B的坐标；

（2）过点A作AC⊥y轴于点C，过点B作直线l∥y轴．动点P从点O出发，以每秒1个单位长的速度，沿O﹣C﹣A的路线向点A运动；同时直线l从点B出发，以相同速度向左平移，在平移过程中，直线l交x轴于点R，交线段BA或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P运动的时间为t秒．

①当t为何值时，以A、P、R为顶点的三角形的面积为8？

②是否存在以A、P、Q为顶点的三角形是等腰三角形？若存在，求t的值；若不存在，请说明理由．

考点分析：

一次函数综合题.

题干分析：

（1）根据图象与坐标轴交点求法直接得出即可，再利用直线交点坐标求法将两直线解析式联立即可得出交点坐标；

（2）①利用S梯形ACOB－S△ACP－S△POR－S△ARB＝8，表示出各部分的边长，整理出一元二次方程，求出即可；

②根据一次函数与坐标轴的交点得出，∠OBN＝∠ONB＝45°，进而利用勾股定理以及等腰三角形的性质和直角三角形的判定求出即可。

解题反思：

此题主要考查了一次函数与坐标轴交点求法以及三角形面积求法和等腰直角三角形的性质等知识，此题综合性较强，利用函数图象表示出各部分长度，再利用勾股定理求出是解决问题的关键。

动态综合问题一直是中考数学压轴题非常喜欢考查的内容，解决此类问题需要考生根据变量之间的关系，对动态几何中的“变量”进行分类讨论,如运动的点、运动的线等等。

考生要想正确解决此类问题，关键在于要抓住点与线的运动和变化,数量之间的关系也随之发生着变化,再把这些“变化”的几何问题就转化为函数问题。

中考数学，一次函数与几何相关综合题，典型例题分析2：

如图，在平面直角坐标系中，以点B（0，8）为端点的射线BG∥x轴，点A是射线BG上的一个动点（点A与点B不重合）．在射线AG上取AD=OB，作线段AD的垂直平分线，垂足为E，且与x轴交于点F，过点A作AC⊥OA，交射线EF于点C．连接OC、CD，设点A的横坐标为t．

（1）用含t的式子表示点E的坐标为_______；

（2）当t为何值时，∠OCD=180°？

（3）当点C与点F不重合时，设△OCF的面积为S，求S与t之间的函数解析式．

考点分析：

一次函数综合题；相似三角形的判定与性质．

题干分析：

（1）由点B坐标为（0，8），可知OB=8，根据线段垂直平分线的定义可知：AE=4，从而求得：BE=t+4，故此点E的坐标为（t+4，8）；

（2）过点D作DH⊥OF，垂足为H．先证明△OBA∽△AEC，由相似三角形的性质可知，EC/AB=AE/OB可求得EC=t/2，从而得到点C的坐标为（t+4，8﹣t/2），因为∠OCD=180°，CF∥DH，可知，OF/OH=FC/DH即从（t+4）/（t+8）=（8﹣t/2）/8而可解得t的值；

（3）三角形OCF的面积=OF•FC/2从而可得S与t的函数关系式．

解题反思：

本题主要考查的是相似三角形的性质和判定，用含字母t的式子表示点C的坐标是解题的关键。

一次函数与几何相关综合问题，题型一般集中在四种题型上面：

1、动态综合问题；

2、分类讨论问题；

3、数形结合相关问题；

4、函数综合问题。

值得注意的是动态和分类讨论经常结合在一起考查学生，“动”中有“分”。

虽然一次函数与几何综合问题比二次函数与几何综合问题相对容易一些，但每年的得分率并不高。通过访问和调查，我们发现考生丢分原因主要有这三个反面：

1、没有准确理清的题目的条件和意思，无法找到解题切入点；

2、分类讨论不全面，答案漏解或多写,考生往往考虑得不够周全而丢分；

三是由于这类题目计算量较大、解答过程长,稍不注意因计算错误而失分。解答一次函数与几何图形综合题的对策有以下三大思想方法。

中考数学，一次函数与几何相关综合题，典型例题分析3：

考点分析：

一次函数综合题．

题干分析：

（Ⅰ）根据折叠的性质得出BM=AM，再由勾股定理进行解答即可；

（Ⅱ）根据勾股定理和三角形的面积得出△AMN，△COM和△ABO的面积，进而表示出S的代数式即可；

（Ⅲ）把S代入解答即可。

解题反思：

此题考查了一次函数的综合问题，关键是利用勾股定理、三角形的面积，三角函数的运用进行分析。

一次函数与几何相关的综合题，具有解题思路广、应用知识广泛、结构新颖、解法无固定模式可循、解法灵活等鲜明特点，我们需要学会从几何问题中确定一次函数解析式，把几何与一次函数知识进行巧妙结合的一种综合运用数学知识的题型。