说到正方形,大家应该都很熟悉,这是一种我们从小学就开始接触的图形,非常的对称和完美。
小学期间因知识有限,并没有对正方形进行深入学习,进入初中之后,教材对正方形相关知识内容进行拓展和深化,成为初中几何学习重要内容之一,也是中考数学几何重点考查对象之一。
什么是正方形?
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。
从正方形的概念,我们可以看出它本质上是平行四边形,是一种特殊的平行四边形,更是一种特殊的矩形和菱形。因此,正方形不仅具有平行四边形所有性质,更加具有自己的特殊性质。
纵观近几年以正方形为载体的中考数学试题,一般都是以基础知识、基本技能、基本数学思想和基本数学活动经验为依托,主要考查考生运用基础知识分析、解决问题的能力。
中考数学,正方形,典型例题分析1:
如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是 .
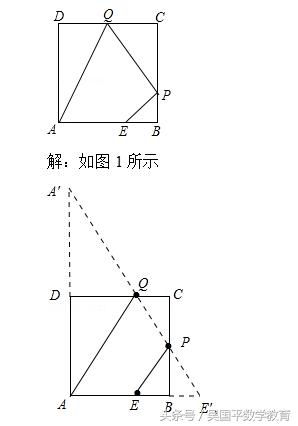
作E关于BC的对称点E′,点A关于DC的对称点A′,
连接A′E′,四边形AEPQ的周长最小,
∵AD=A′D=3,BE=BE′=1,
∴AA′=6,AE′=4.
∵DQ∥AE′,D是AA′的中点,
∴DQ是△AA′E′的中位线,
∴DQ=AE′/2=2;CQ=DC﹣CQ=3﹣2=1,
∵BP∥AA′,
∴△BE′P∽△AE′A′,BP/6=1/4
∴BP/AA’=BE’/AE’,即BP/6=1/4,BP=3/2,CP=BC﹣BP=3﹣3/2=3/2,
S四边形AEPQ=S正方形ABCD﹣S△ADQ﹣S△PCQ﹣SBEP
=9﹣AD•DQ/2﹣CQ•CP/2﹣BE•BP/2
=9﹣(3×2)/2﹣1×3/2×1/2﹣×1×3/2×1/2=9/2,
故答案为:9/2.
考点分析:
轴对称-最短路线问题;正方形的性质;计算题.
题干分析:
根据最短路径的求法,先确定点E关于BC的对称点E′,再确定点A关于DC的对称点A′,连接A′E′即可得出P,Q的位置;再根据相似得出相应的线段长从而可求得四边形AEPQ的面积。
解题反思:
本题考查了轴对称,利用轴对称确定A′、E′,连接A′E′得出P、Q的位置是解题关键,又利用了相似三角形的判定与性质,图形分割法是求面积的重要方法。
中考数学,正方形,典型例题分析2:
如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:

解:∵四边形ABCD是正方形,
∴∠GAD=∠ADO=45°,
由折叠的性质可得:∠ADG=∠ADO/2=22.5°,
故①正确.
∵由折叠的性质可得:AE=EF,∠EFD=∠EAD=90°,
∴AE=EF<BE,
∴AE<AB/2,
∴>2,
故②错误.
∵∠AOB=90°,
∴AG=FG>OG,△AGD与△OGD同高,
∴S△AGD>S△OGD,
故③错误.
∵∠EFD=∠AOF=90°,
∴EF∥AC,
∴∠FEG=∠AGE,
∵∠AGE=∠FGE,
∴∠FEG=∠FGE,
∴EF=GF,
∵AE=EF,
∴AE=GF,
故④正确.
∵AE=EF=GF,AG=GF,
∴AE=EF=GF=AG,
∴四边形AEFG是菱形,
∴∠OGF=∠OAB=45°,

考点分析:
四边形综合题.
题干分析:
①由四边形ABCD是正方形,可得∠GAD=∠ADO=45°,又由折叠的性质,可求得∠ADG的度数;
②由AE=EF<BE,可得AD>2AE;
③由AG=GF>OG,可得△AGD的面积>△OGD的面积;
④由折叠的性质与平行线的性质,易得△EFG是等腰三角形,即可证得AE=GF;
⑤易证得四边形AEFG是菱形,由等腰直角三角形的性质,即可得BE=2OG;
⑥根据四边形AEFG是菱形可知AB∥GF,AB=GF,再由∠BAO=45°,∠GOF=90°可得出△OGF时等腰直角三角形,由S△OGF=1求出GF的长,进而可得出BE及AE的长,利用正方形的面积公式可得出结论.
解题反思:
此题考查的是四边形综合题,涉及到正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识.此题综合性较强,难度较大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用。

认真掌握以下这些正方形的性质:
1、具有平行四边形、矩形、菱形的一切性质;
2、正方形的四个角都是直角,四条边都相等;
3、正方形的两条对角线相等,并且互相垂直平分,每一条对角线平分一组对角;
4、正方形是轴对称图形,有4条对称轴;
5、正方形的一条对角线把正方形分成两个全等的等腰直角三角形,两条对角线把正方形分成四个全等的小等腰直角三角形;
6、正方形的一条对角线上的一点到另一条对角线的两端点的距离相等。
中考数学,正方形,典型例题分析3:
如图,点P是正方形ABCD对角线AC上一动点,点E在射线BC上,且PB=PE,连接PD,O为AC中点.
(1)如图1,当点P在线段AO上时,试猜想PE与PD的数量关系和位置关系,不用说明理由;
(2)如图2,当点P在线段OC上时,(1)中的猜想还成立吗?请说明理由;
(3)如图3,当点P在AC的延长线上时,请你在图3中画出相应的图形(尺规作图,保留作图痕迹,不写作法),并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.
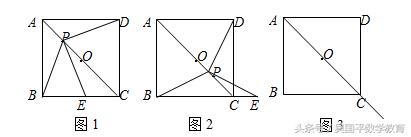
解:(1)当点P在线段AO上时,
PE与PD的数量关系和位置关系分别为:PE=PD,PE⊥PD;
(2)∵四边形ABCD是正方形,AC为对角线,
∴BA=DA,∠BAP=∠DAP=45°,
∵PA=PA,
∴△BAP≌△DAP(SAS),
∴PB=PD,
又∵PB=PE,
∴PE=PD.
(i)当点E在线段BC上(E与B、C不重合)时,
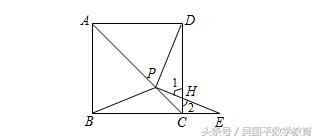
∵PB=PE,
∴∠PBE=∠PEB,
∴∠PEB=∠PDC,
而∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
∴∠DPE=360°﹣(∠BCD+∠PDC+∠PEC)=90°,
∴PE⊥PD.
(ii)当点E与点C重合时,点P恰好在AC中点处,此时,PE⊥PD.
(iii)当点E在BC的延长线上时,如图.
∵∠PEC=∠PDC,∠1=∠2,
∴∠DPE=∠DCE=90°,
∴PE⊥PD.
综合(i)(ii)(iii),PE⊥PD;
考点分析:
正方形的性质;全等三角形的判定与性质;等腰三角形的性质。
题干分析:
(1)根据点P在线段AO上时,利用三角形的全等判定可以得出PE⊥PD,PE=PD;
(2)利用三角形全等得出,BP=PD,由PB=PE,得出PE=PD,要证PE⊥PD;从三方面分析,当点E在线段BC上(E与B、C不重合)时,当点E与点C重合时,点P恰好在AC中点处,当点E在BC的延长线上时,分别分析即可得出;
(3)利用PE=PB得出P点在BE的垂直平分线上,利用垂直平分线的性质只要以P为圆心,PB为半径画弧即可得出E点位置,利用(2)中证明思路即可得出答案.
解题反思:
此题主要考查了正方形的性质以及全等三角形的判定与性质和尺规作图等知识,此题涉及到分类讨论思想,这是数学中常用思想同学们应有意识的应用。

如何判定一个四边形是不是正方形?掌握好这些正方形判定定理:
1、判定一个四边形是正方形的主要依据是定义,途径有两种:
先证它是矩形,再证有一组邻边相等。
先证它是菱形,再证有一个角是直角。
2、判定一个四边形为正方形的一般顺序如下:
先证明它是平行四边形;
再证明它是菱形(或矩形);
最后证明它是矩形(或菱形)。
中考数学,正方形,典型例题分析4:
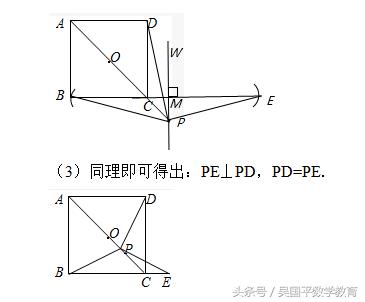
在平面直角坐标系xOy中,边长为a(a为大于0的常数)的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.
(1)当∠BAO=45°时,求点P的坐标;
(2)求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在∠AOB的平分线上;
(3)设点P到x轴的距离为h,试确定h的取值范围,并说明理由.

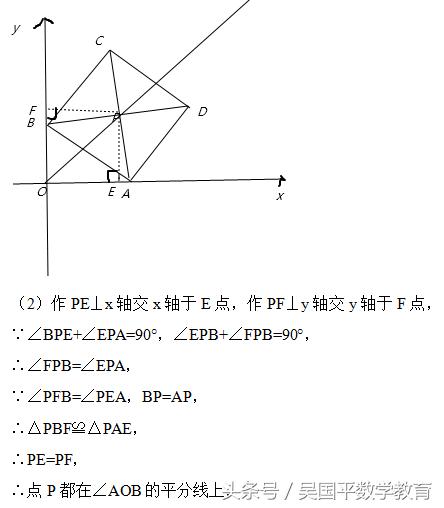
(3)因为点P在∠AOB的平分线上,所以h>0.
考点分析:
正方形的性质;坐标与图形性质;全等三角形的判定与性质;解直角三角形;几何动点问题;几何综合题。
题干分析:
(1)当∠BAO=45°时,因为四边形ABCD是正方形,P是AC,BD对角线的交点,能证明OAPB是正方形,从而求出P点的坐标.
(2)过P点做x轴和y轴的垂线,可通过三角形全等,证明是角平分线.
(3)因为点P在∠AOB的平分线上,所以h>0.
解题反思:
本题考查里正方形的性质,四边相等,四角相等,对角线互相垂直平分,且平分每一组对角,以及坐标与图形的性质,全等三角形的判定和性质,解直角三角形等知识点。
 加载中,请稍侯......
加载中,请稍侯......
精彩评论