2020年河南中考21题的几点想法

本是压轴题的抛物线在2020年被前移到了21题（倒数第三），难度自然下降了不少，第一问没有变化，第2问成了“秒杀”，所考查的知识与能力并没有降低，更强化了初高中的衔接，体现出了一个明显的倾向：“思维多一点，运算少一点”。

方法一：代数法求值域

方法二：数形结合

此题明显考查的是函数的值域问题（纵坐标的取值范围问题），要充分理解函数定义域和值域的几何特征，即可观察秒杀。函数的定于域、值域的几何意义分别是图像上的所有点在轴上的投影。

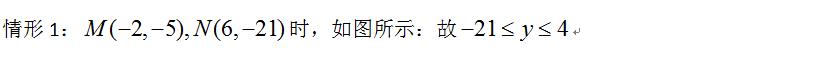
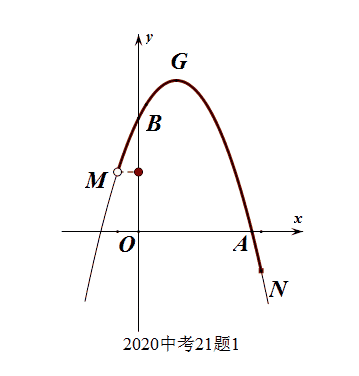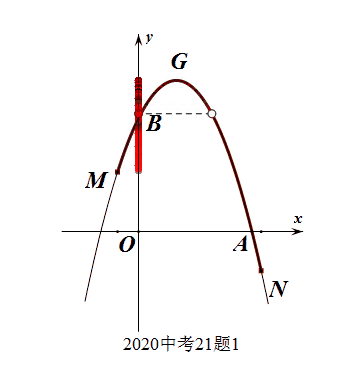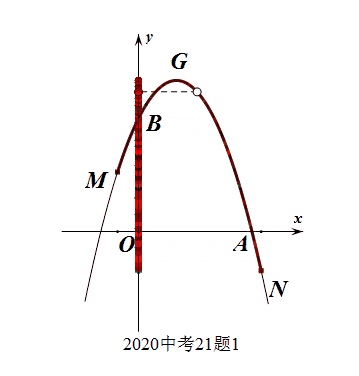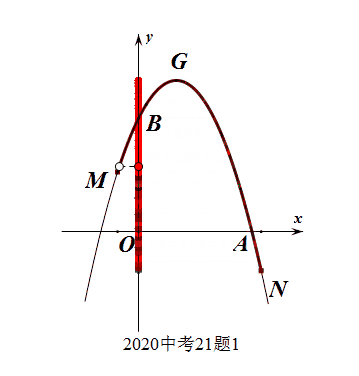
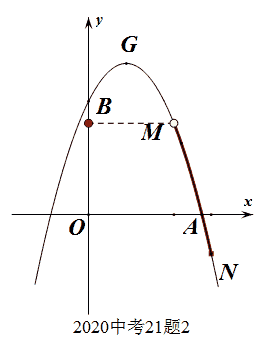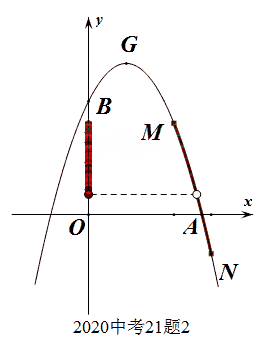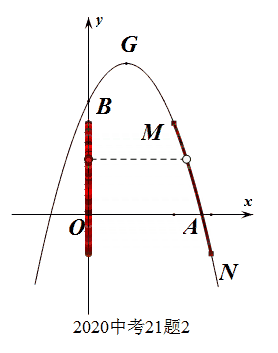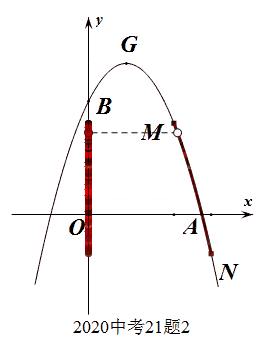
此处的数形结合是在基础知识、基本能力达到一定层次，产生了一定的数感、图感之后的“随心所欲”。

几点想法：

1.理解命题人的命题意图，明确考查目的

本题的解决方法不拘一格，但命题人的意图是什么？是偏重于运算还是偏重于思维？但凡一个稍微综合的的数学问题，都要经历定性思维和定量运算两个阶段，前者是基础，思维不通畅不知道运算什么，思维不到位会加大运算量，耽误时间不说，还提高了运算失败的概率，这是在课堂上经常见到的现象。后者是，通过运算可以检验思维的正确性，达到解决问题的目的。在科技高度发达的今天，前者显得更重要，于是就有了“思维多一点，运算少一点”的说法。一个问题就像一个平衡系统，思维多了，运算自然就少了；思维少了，运算必然加大，这也是自然界中平衡原则的完美体现。

2.对取值范围的理解，学生停留在哪个层次？

这就是数形结合问题，“数”与“形”完美结合必然提升思维的深度、广度和高度，必然为“运算少一点”提供保障。怎样培养学生的数形结合能力，是说说就行的吗？当然不是！需要学生去感知，让学生去“见识”。只有见过的东西，才能够真正的感知到，否则就是主观臆断。怎样把老师大脑中的东西让学生看到呢？就是利用数学工具，结合电脑屏幕来直观的显示教师大脑“屏幕”中的东西，长此以往的熏陶、强化，以实现“认识、理解、运用”的效果（比如本文中的动画演示）。

3.分层教学的问题

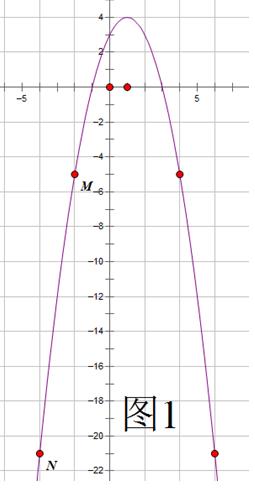
分层教学常可以理解为对不同认知水平的学生采取不同的教学手段和教学内容，而事实上还要关注对同一学生在不同的层次阶段，不同的学习场合采取不同的方法。例如在本题中所体现的作图问题，是采用精准作图，还是特征图像呢？如果找到点M、N的准确位置，就会做出一个非常“大”的图形，可能浪费“人力、物力、财力”,在有限的视觉范围内难以“容”下M、N两点（图1）。

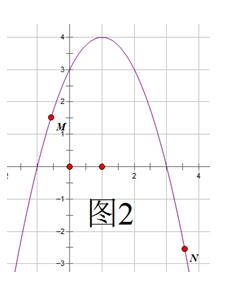
而本题的本质在于有两点，故只需找出相对关系不变的两点就行（刻画出特征），不用刻意追求它的准确度（图2）。

也就是说在刚开始学习作图（不管是解答还是选填）时要规范严谨，在综合复习阶段（思维需要）就需要反映特征了。还有一种现象：高中的学生（高三学生不在少数）借助函数图象解决问题时，会利用大量的时间做出一个标准的平面直角坐标系，刻度线、刻度值（正负半轴）应有尽有，而真正需要使用的却是偏居一隅的“小图像”，无用的部分却占据着大量的空间.

基础打好了，思维灵活了，思想解放了，才能够“为所欲为”！