高中数学当中有许多听讲的时候很懂，看起来也都会，但是就是一做就错的题目。其中立体几何中的二面角问题就是其中之一。这次我们就来讲讲二面角问题通常应当如何解答，才能避免考试的时候出现错误。

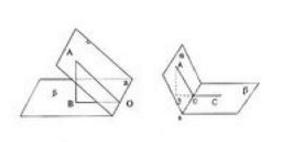
一、二面角的由来及基础定义

二面最初是由两面相交的问题引申出来的一个问题。

由于二面相交使得两个平面相对的关系出现几种情况，其中比较特殊的一种情况就是垂直。

而二面角就是证明两面垂直的一个重要的证明途径。

当面a与面b相较于直线L的时候，如果有在a面内的直线La⊥L与点K，且有在b面的直线Lb⊥L与点K。如果同时La⊥Lb，那么我们就可以推导出面a⊥面b。

二、在解决二面角问题是常见的错误方式

除了在二面垂直方面，二面角的性质有这很特殊的意义之外。

我们在平时解题过程中往往大多会碰上二面成一定角度的情况（常见的有30°，45°，60°等）。

然后通过从一个面向另一个面投影来进行出题。也有一些是通过已知条件求解二面角值的问题。

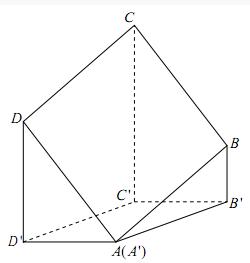
例如上图，就是一道曾经出现在高考中的题目图，问题的第一问就是求面ABCD与面A'B'C'D‘的二面角。

不少同学的错解都是直接联结AC,A'C'来解三角形，导致结果出现错误。

而这道题的第一问正解则是通过BB'（或DD‘）做延长线，然后通过BB'（或DD‘）分别作两面交线的垂线段再进行解题。

三、解决二面角问题的正确顺序

二面角的问题可能出现在各类集合题目中，看戏繁杂无规律。但是实际上也正是由于二面角的特殊性，其解题存在着一定的技巧。

（1）读题时注意特殊角度

在求解题目的过程中，已知条件告知的特殊角度（30°，45°，60°）等往往是题目的主要突破口。

尤其是作为大题第一问出现的时候。由于高中知识基本很难涉及到其他角度（部分竞赛题目会涉及15°和75°）的多重二面角计算。所以一定要千万注意特殊角度的调件。

这些条件不一定会字面给出，比如给三角形的三边长之类的条件可以推知某个角的大小。

（2）合理利用隐藏调件

不少题目利用几何形状的一些性质给予我们特殊的意义。

比较浅显的如告知正三角形，那么就可以知道几个角的大小，告知正方体就可以推断出垂直。

另一部分略有深度的隐藏条件则需要我们在做题过程中通过运用来掌握。

我们这里举个例子：2个不平行、不垂直且不重合的平面a,b交于线L，a面中有一个正方形ABCD，4个点均在L的同一侧，4个点在面b上的4个投影点分别为A'B'C'D。

当我们得知这些结论的时候，其实就可以发现A'B'C'D实际上是个平行四边形。（当AC或BD平行于L的特殊情况下，投影的形状是菱形。）

而这种隐藏条件往是我们解题灵光一现的重要突破口。

（3）三垂线法解题

课堂上老师们应对二面角的方法往往就是这个“三垂线”法。但是实际上很多学生听后都有类似的疑问：我怎么知道通过哪个点来做垂线呢？或者是解题更快呢（有的题目选错点解题步骤会很繁琐）？

这里给大家分享一个略显笨拙却行之有效的方法：

1、看看题目已知条件中是否有垂直或特殊角度的信息，如果有就往下接着看，如果没有，请直接到第6步；

2、将二面角问题所涉及的点，依次列出；

3、分别通过读题看看这些点分别与多少个已知条件相关，从高往低排列；

4、从上往下筛，比如从点A开始，如果有条件与点A相关且涉及到垂直、特殊角度（例如AB⊥CD）等条件，我们就要关注下点B了。往往点B就是解题的关键点；

5、如果点A不涉及到特殊角度，那么我们查找第二个条件，依此类推；

6、如果已知条件中没有垂直或特殊角度的点，我们就要选择2个平面之一作为底面（被投影面），而另一面作为投影面；

7、选择投影面上与两面交线最近，且与已知条件相关较多的一个点，过此点做被投影面的垂线段。往往会成为这个题目的解题关键点。