方法与技巧：

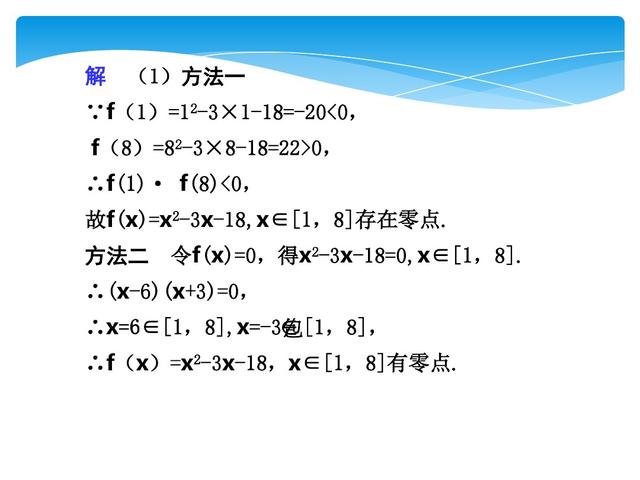
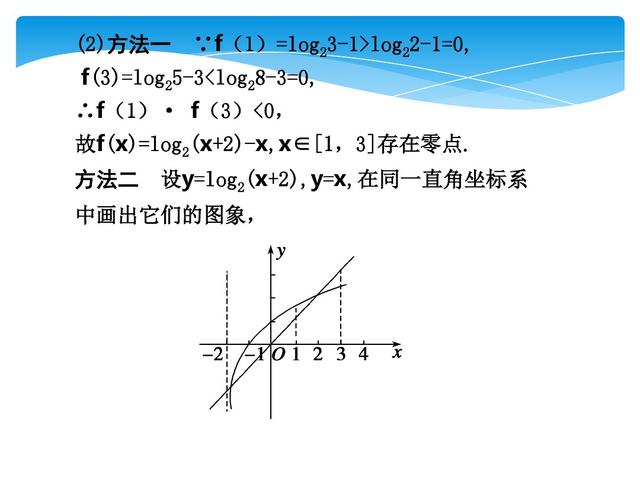
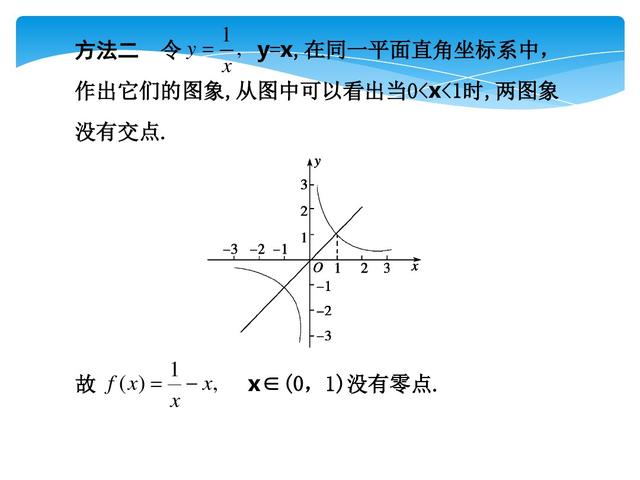
一、函数零点的判定常用的方法：①零点存在性定理；②数形结合；③解方程f（x）=0

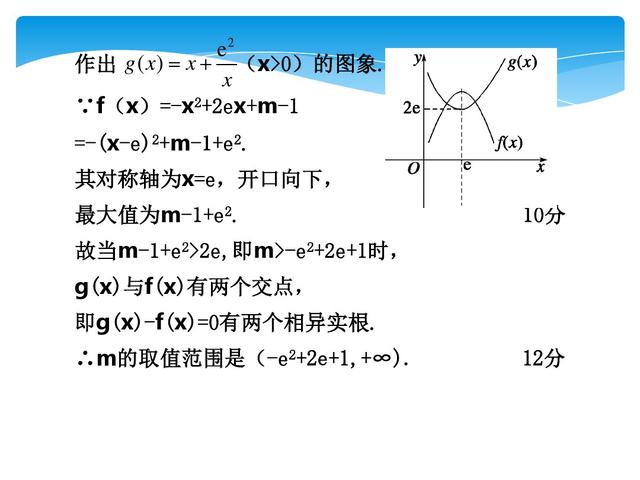
二、研究方程f（x）=g（x）的解，实质就是研究G（x）=f（x）-g（x）的零点

三、二分法是求方程的根的近似值的一种计算方法，其实质是通过不断地“取中点”来逐步缩小所在的范围，当达到一定的精确度要求时，所得区间的任一点就是这个函数零点的近似值。

失误与防范：

（1）函数的零点是一个实数，当函数的自变量取这个实数时，其函数值等于零。

（2）函数的零点也就是函数y=f（x）的图像与x轴的交点的横坐标

（3）一般我们只讨论函数的实数零点

（4）函数的零点不是点，是方程f（x）=0的根