中考数学解题思路及技巧：方程思想

• 方程思想是从分析问题的数量关系入手，适当设定未知数，把所研究的数学问题中已知量和未知量之间的数量关系，转化为方程或方程组的数学模型，从而使问题得到解决的思维方法。

• 用方程思想解题的关键是利用已知条件或公式、定理中的已知结论构造方程(组)。这种思想在代数、几何及生活实际中有着广泛的应用。

  

• 典型例题：如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB，延长DA与⊙O的另一个交点为E，连接AC，CE。

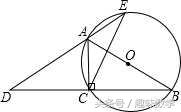
• （1）求证：∠B=∠D；（2）若AB=4，BC-AC=2，求CE的长．

• 思路分析：

（1）由AB为⊙O的直径，易证得AC⊥BD，又由DC=CB，根据线段垂直平分线的性质，可证得AD=AB，即可得：∠B=∠D；

（2）首先设BC=x，则AC=x-2，由在Rt△ABC中，AC2+BC2=AB2，可得方程：（x-2）2+x2=42，解此方程即可求得CB的长，继而求得CE的长。

• 解答：

（1）证明：

∵AB为⊙O的直径

∴∠ACB=90°

∴AC⊥BC

∵DC=CB

∴AD=AB

∴∠B=∠D

（2）解：设BC=x，则AC=x-2， 在Rt△ABC中，AC2+BC2=AB2

∴（x-2）2+x2=42，

解得：x1=1+7，x2=1-7（舍去）

∵∠B=∠E，∠B=∠D

∴∠D=∠E

∴CD=CE

∵CD=CB

∴CE=CB=8

• 点评：此题考查了圆周角定理、线段垂直平分线的性质、等腰三角形的判定与性质以及勾股定理等知识．此题难度适中，注意掌握方程思想与数形结合思想的应用．