高中数列求和最全的方法

一、利用常用求和公式求和

利用下列常用求和公式求和是数列求和的最基本最重要的方法.

二、错位相减法求和

这种方法是在推导等比数列的前n项和公式时所用的方法，这种方法主要用于求数列{an·　bn}的前n项和，其中{ an }、{ bn }分别是等差数列和等比数列.

三、反序相加法求和

这是推导等差数列的前n项和公式时所用的方法，就是将一个数列倒过来排列（反序），再把它与原数列相加，就可以得到n个

.

四、分组法求和

有一类数列，既不是等差数列，也不是等比数列，若将这类数列适当拆开，可分为几个等差、等比或常见的数列，然后分别求和，再将其合并即可.

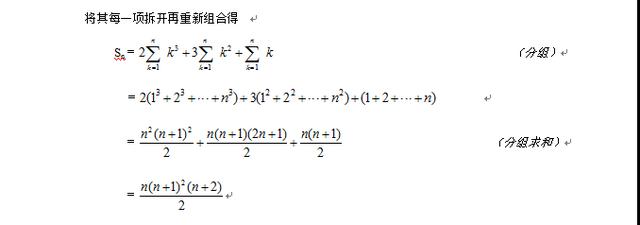
五、裂项法求和

这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项（通项）分解，然后重新组合，使之能消去一些项，最终达到求和的目的. 通项分解（裂项）如：

六、分段求和法（合并法求和）

针对一些特殊的数列，将某些项合并在一起就具有某种特殊的性质，因此，在求数列的和时，可将这些项放在一起先求和，然后再求Sn.