知识点:
1、三角形的概念由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
组成三角形的线段叫做三角形的边;
相邻两边的公共端点叫做三角形的顶点;
相邻两边所组成的角叫做三角形的内角,简称三角形的角。
2、三角形中的主要线段
(1)三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点间的线段叫做三角形的角平分线。
(2)在三角形中,连接一个顶点和它对边的中点的线段叫做三角形的中线。
(3)从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高)。
3、三角形的稳定性三角形的形状是固定的,三角形的这个性质叫做三角形的稳定性。三角形的这个性质在生产生活中应用很广,需要稳定的东西一般都制成三角形的形状。
4、三角形的特性与表示三角形有下面三个特性:
(1)三角形有三条线段
(2)三条线段不在同一直线上
(3)首尾顺次相接
注:三角形是封闭图形
三角形用符号“D”表示,顶点是A、B、C的三角形记作“DABC”,读作“三角形ABC”。
5、三角形的分类
三角形按边的关系分类如下:
三角形分为不等边三角形和等腰三角形,其中等腰三角形又分为底和腰不相等的等腰三角形和等边三角形
三角形按角的关系分类如下:
三角形按角可分为直角三角形和斜三角形,其中直角三角形是有一个角为直角的三角形;斜三角形分为锐角三角线(三个角都为锐角的三角形)和钝角三角形(有一个角为钝角的三角形)。
把边和角联系在一起,我们又有一种特殊的三角形:等腰直角三角形。它是两条直角边相等的直角三角形。
6、三角形的三边关系定理及推论
(1)三角形三边关系定理:三角形的两边之和大于第三边。
推论:三角形的两边之差小于第三边。
(2)三角形三边关系定理及推论的作用:
①判断三条已知线段能否组成三角形
②当已知两边时,可确定第三边的范围。
③证明线段不等关系。
7、三角形的内角和定理及推论
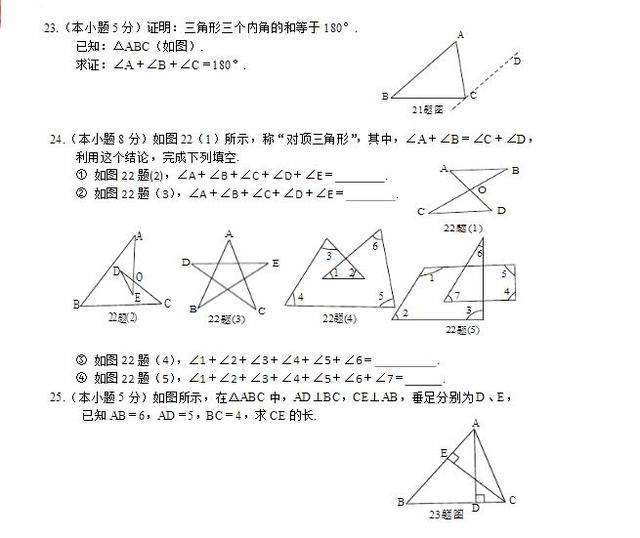
三角形的内角和定理:三角形三个内角和等于180°。
推论:
①直角三角形的两个锐角互余。
②三角形的一个外角等于和它不相邻的来两个内角的和。
③三角形的一个外角大于任何一个和它不相邻的内角。
注:在同一个三角形中:等角对等边;等边对等角;大角对大边;大边对大角。
8、三角形的面积= 1/2×底×高
练习题


答案:
一、选择题
1、C 2、B 3、A 4、A 5、C 6、B 7、A 8、B 9、C 10、A 11、C 12、C
二、填空
13、180、360 ;14、5 ;15、18 ;16、10˚;
17、∠A=30°;∠B=60°;∠C90°
18:n-3;n-2
19、15;20
20、18;4n+2
21、原式=b+c-a+c+a-b+c-a+b=3c+b-a
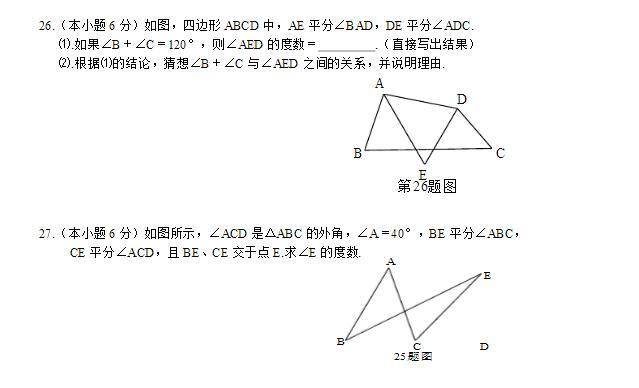
22、7个三角形;以E为顶点的角有四个分别为:
23、利用平行线的性质,过C点作AB的平行线,两直线平行内错角相等
24、(1)180˚ (2)180˚ (3)360˚ (4)540˚
25、0.5×AB×CE=0.5×AD×BC CE=10/3
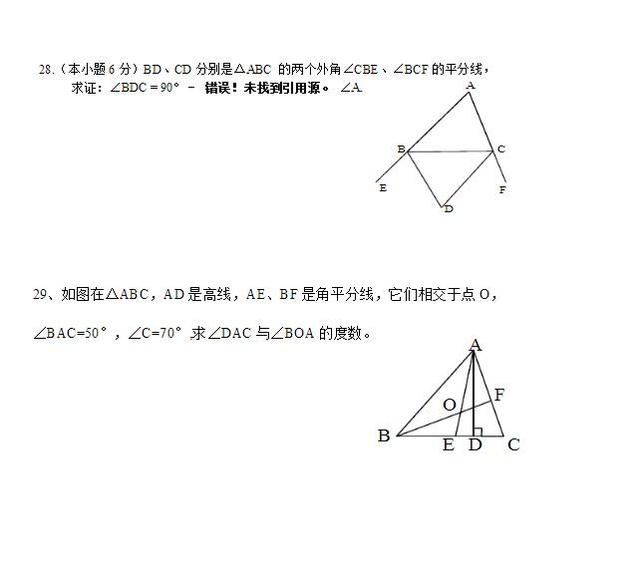
26、(1)60˚ (2)
27、∠A=40˚ ∠E=20˚
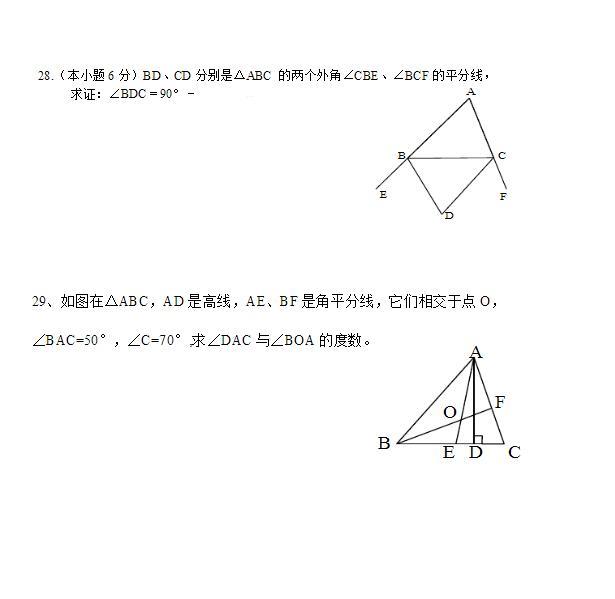
28、略
29、∠DAC=20,∠BOA=125
 加载中,请稍侯......
加载中,请稍侯......
精彩评论