初中数学“函数”概念之我见，难点在哪里，如何破解？

初中代数“数与式”是基础，其上有三个并行的分支“方程”、“不等式”、"函数"。说它们并行，是因为学习方程的定义不依赖不等式和函数，函数的定义不依赖方程和不等式，虽然不等式类比方程学起来更容易，但不等式的概念与理论并不需要依赖于方程，因此说它们是并行的，它们的共同基础就是数与式。

一、尽管三者是并行的，但学习起来确实是函数最难。原因有哪些呢？

1：初中数学，大多数概念都是有前面的知识和学习经验铺垫、类比的，比如方程有小学的基础，不等式有等式与方程的基础。唯独函数是个全新的概念，没有任何知识和经验可以借鉴。

2：数学中大多数概念都是可以顾名思义的，比如不等式（由不等号连接的式子）、相反数（只有符号不同的数）等等。而函数这个概念，由于翻译的原因，以及函数本身的意义比较抽象，很难有顾名思义的词语去表示。到了高中，函数其实是一种映射，映射这个概念就比较顾名思义了。

3：函数表示两个变量之间的关系，但它是有顺序的。对于自变量x的每一个确定的值，y都有唯一确定的值，则称y是x的函数，x是自变量。注意，不能弄反了说成x是y的函数。而其它表示关系的概念，通常是相互的，比如相反数，2是-2的相反数，反过来，-2也是2的相反数。

4：方程、不等式总是以式（等式、不等式）的形象出现，而函数的“长相”多种多样（图象法、列表法、解析法），并不是所有的函数都以式的形象出现，主要是根本就无法以式的形象出现，如温度T（℃）和时间t的函数关系太复杂不可能用式子表达出来。

二、函数概念教学设想：

大多数概念都是抽象得到的，因此先举3个例子如下：

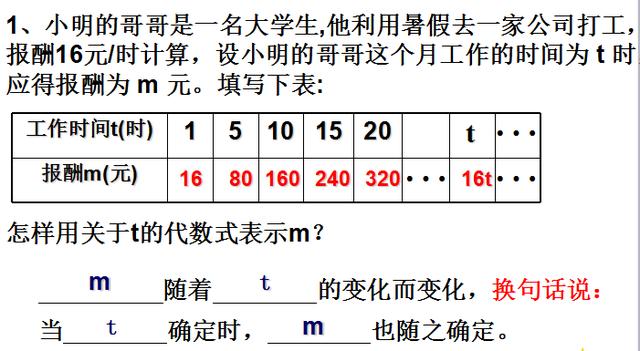
世界万事万物都是相互联系的。填空第一行，感受两个变量之间的依赖关系，注意顺序不能反。《换句话说》这四个字很重要，把依赖关系进一步具体化、精确化，是如何依赖的？

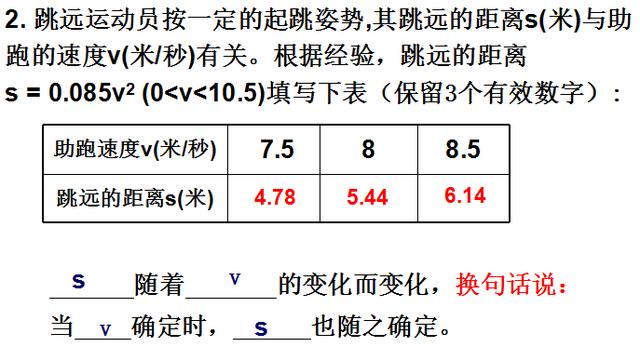
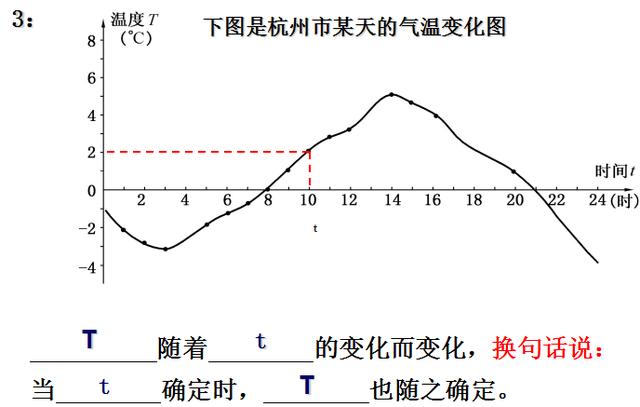
三个例子结束，找共同点，归纳抽象得出概念，形成定义

可作板书设计如下

巩固练习：

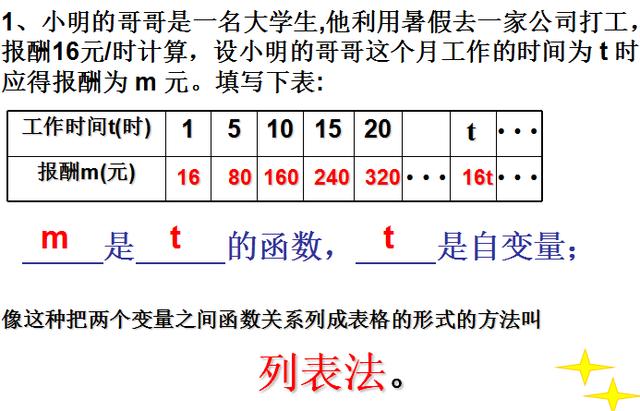
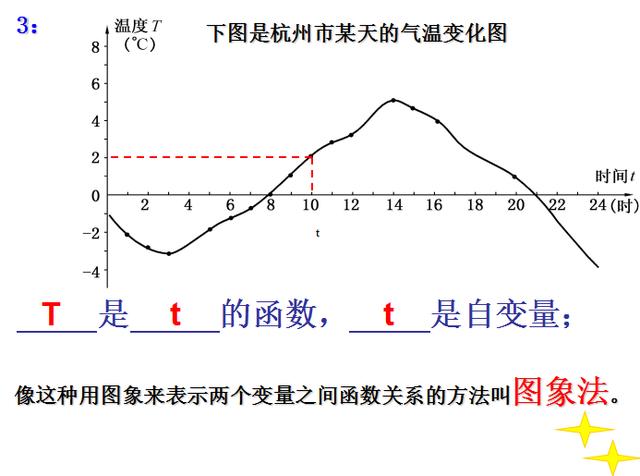
说明：函数解析式也可叫函数表达式、函数关系式、函数式。

判断两个变量是否构成函数与函数的“长像”无关，不管哪一种“长像”，都要满足对于自变量x的每一个确定的值，y相应的都有唯一确定的值。

上面的3个例子一个函数一种表示法，下面出示一个函数同时用3种方法表示：

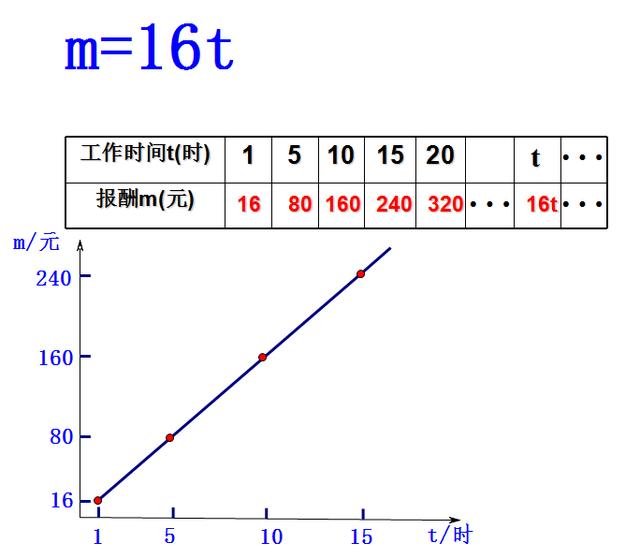
三、类比方程，熟记名词

对于2x-1=10，x叫做未知数，该方程可以称做关于未知数"x"的方程，式子可以叫做方程式。对于y=2x-1，x叫做自变量，可称 关于自变量x的函数，式子可以叫做函数式。方程与函数在名称上，是可以类比去记的。二者又可以相互转化，当把x与y看作未知数，则y=2x-1是二元一次方程。当把x，y看作变量，则y=2x-1是函数。