中考中有关因式分解的考点解析

因式分解一直是中考中的一个非常重要的考点，深受出题者的青睐，本文将归纳中考中关于因式分解常考的几种题型进行剖析。

考点一 考查因式分解的概念

解选D．

分析：本题需注意因式分解是把一个多项式化为几个整式的积的形式。除了根据概念来外，还可以根据因式分解与整式乘法的互逆关系来判断．

考点二 考查分解因式的方法

分解因式的方法：(1) 直接提公因式法；(2) 公式法；(3) 提公因式法与公式法的综合应用;(4)十字相乘法．其中以第 (3) 种方法为考查重点．

1、直接提公因式法

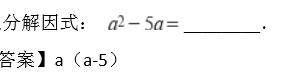
点评：本题直接将公因式a提出即可。

2、 公式法

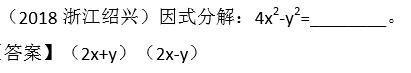
点评：本题直接运用平方差公式即可

3、提公因式法与公式法的综合应用

点评：本题先通过提取公因式y后，剩余部分再通过平方差公式分解即可。

4、十字相乘法

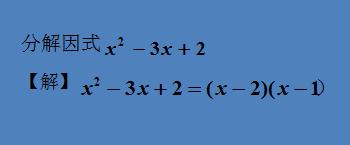
三、考查分解因式的应用

与分解因式应用有关的考题主要涉及以下几个方面：(1) 根据分解因式进行变形求值；(2) 根据分解因式变形说理等．

对任意一个四位数n,如果千位与十位上的数字之和为9，百位与个位上的数字之和也为9，则称n为“极数”.

（1）请任意写出三个“极数”；并猜想任意一个“极数”是否是99的倍数，请说明理由；

（2）如果一个正整数a是另一个正整数b的平方，则称正整数a是完全平方数，若四位数m为“极数”，记D（m）=m/33.求满足D（m）是完全平方数的所有m.