锐角三角函数是初中数学中非常重要的一个章节,也是中考中必考的内容。在学习这章节内容是首先要充分理解三角函数的意义,熟记三角函数的数值,然后能够熟练运用三角函数解实际问题。本文将中考中常考的5个考点进行列举分析。
考点一:锐角三角函数的概念
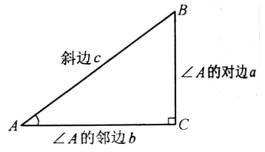
初中学习的锐角三角函数值的定义方法是在直角三角形中定义的,锐角三角函数可表示如下:
正弦(sin)等于对边比斜边;sinA=a/c
余弦(cos)等于邻边比斜边;cosA=b/c
正切(tan)等于对边比邻边;tanA=a/b
余切(cot)等于邻边比对边;cotA=b/a
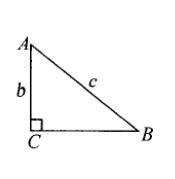
例1:在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,则下列各项中正确的是( )
A.a=c·sinB B.a=c·cosB C.a=c·tanB D.以上均不正确
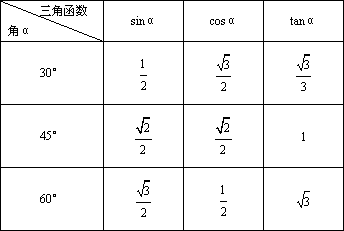
考点二 特殊三角函数值的应用
例2:在△ABC中,若∣cosA-1/2∣+(1-tanB)²=0,则∠C的度数是( ).
A.45° B.60° C.75° D.105°
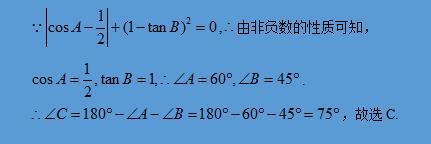
对于特殊角的三角函数值,要善于从两个方面去应用:(1)已知一个特殊角,要知道这个特殊角的三角函数值;(2)已知一个特殊角的三角函数值,要知道这是特殊角的度数.利用非负数的性质,可以由一个等式构造出方程(组)来解决问题,这是解决由一个等式求多个未知数值问题的常用解题策略,要深刻体会,学会灵活运用.
考点三 解直角三角形
例3一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是( )(结果保留小数点后两位)(参考数据:√3≈1.732,√2≈1.414)
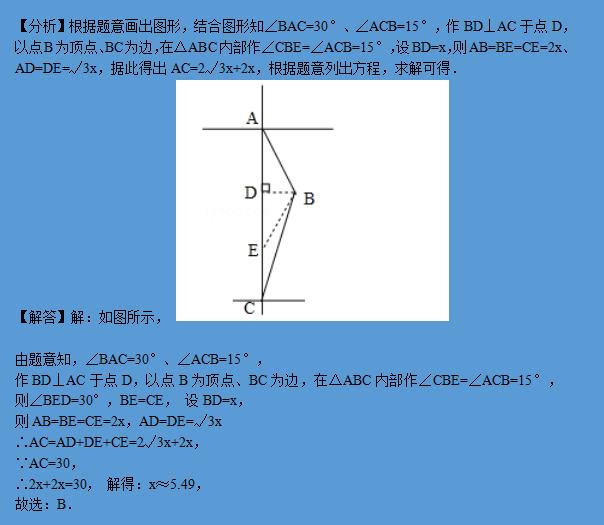
考点四 解非直角三角形
非直角三角形可以通过添加辅助线构造出直角三角形来解决.
例4 △ABC中,AB=4,BC=3,∠BAC=30°,则△ABC的面积为___________.
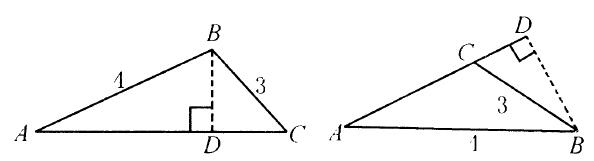

考点五 应用解直角三角形的知识解决实际问题
例:直升飞机在跨江大桥AB的上方P点处,此时飞机离地面的高度PO=450米,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为α=30°,β=45°,求大桥的长AB.
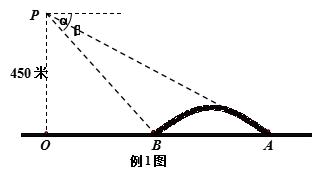


 加载中,请稍侯......
加载中,请稍侯......
精彩评论