中考中《二次函数》压轴题常考类型合集

二次函数压轴题是历年中考的热点与难点，其中动点问题是热点中的热点，此类问题主要有两类:一是动点函数图象问题;二是借助动点和三角形、四边形相结合的问题.解答动点问题时，要把问题拆分，分清动点在不同位置运动或不同时间段运动时对应的函数关系式，进而确定函数图象。

考法一：二次函数的动点问题

例1 ( 宿迁)如图1，在平面直角坐标系中，抛物线y=x²-2x-3交x轴于A,B两点(点A在点B的左侧)，将该抛物线位于x轴上方的曲线记作M，将该抛物线位于x轴下方的部分沿X轴翻折，翻折后所得曲线记作N，曲线N交y轴于点C，连接AC,BC.

(1)求曲线N所在抛物线相应的函数表达式.

(2)求△ABC外接圆的半径.

(3)点P为曲线M或曲线N上的一个动点，点Q为x轴上的一个动点，若以点B,C,P,Q为顶点的四边形是平行四边形，求点Q的坐标.

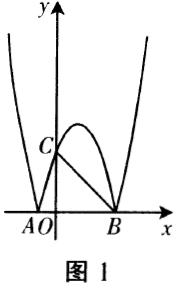
分析:(1)由已知抛物线可求得点A,B两点的坐标及顶点坐标，利用对称性可求得点C的坐标，利用待定系数法可求得曲线N的函数表达式.

(2)由外接圆的定义，可知圆心即为线段BC与AB的垂直平分线的交点，即直线y=x与抛物线对称轴的交点，可求得外接圆的圆心，再利用勾股定理可求得半径的长.

(3)设Q(x,0)，当BC为平行四边形的边时，有BQ∥BC且BQ=BC，从而可用x表示出P点的坐标，代入抛物线的函数表达式可得到关于x的方程，从而可求得Q点的坐标;当BC为平行四边形的对角线时，由点B,C的坐标，可求得平行四边形的对称中心的坐标，从而可表示出P点的坐标，代入抛物线的函数表达式可得到关于x的方程，从而求得Q点的坐标.

评注:本题为二次函数的综合应用问题，涉及待定系数法、对称的性质、三角形的外心、勾股定理、平行四边形的性质、方程思想及分类讨论思想等知识.在(1)中，确定点的坐标是解题的关键;在(2)中，确定外心的位置和坐标是解题的关键;在(3)中，确定只点的位置是解题的关键.

考法二:二次函数的存在点问题

例2 (安顺)如图3甲，直线y=-x+3与x轴、y轴分别交于点B,C，经过B,C两点的抛物线y=x²+bx+c与x轴的另一个交点为A，顶点为P.

(1)求该抛物线的函数表达式.

(2)在该抛物线的对称轴上是否存在点M,使以CPM为顶点的三角形为等腰三角形?若存在，请直接写出所有符合条件的点M的坐标;若不存在，请说明理由.

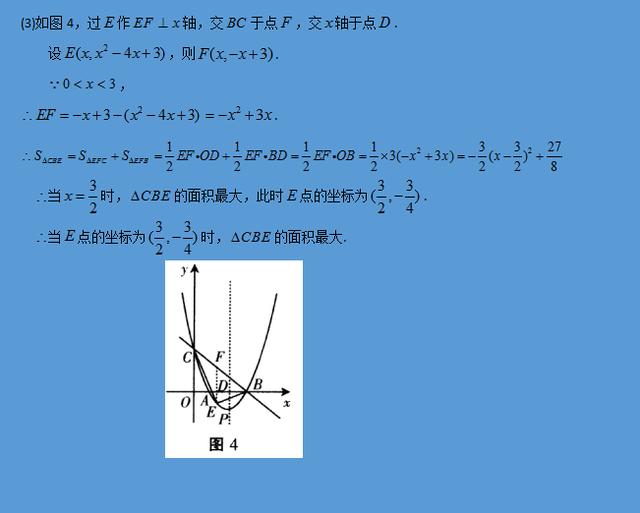
(3)当0＜x＜3时，在抛物线上求一点E，使△CBE的面积有最大值(图3乙和图3丙供画图探究使用).

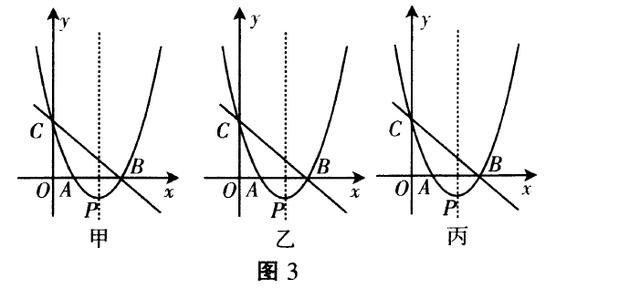
分析:(1)由直线的函数表达式，可得B,C的坐标，利用待定系数法可求得抛物线的函数表达式.

(2)由抛物线的函数表达式可求得P点的坐标及对称轴，可设出M点的坐标，表示出MC,MP,PC的长，分MC=MP,MC=PC,MP=PC三种情况，可分别得到关于M点坐标的方程.，可求得M点的坐标.

(3)过E作EF⊥x轴，交直线BC于点F，交F轴于点D，可设出E点的坐标，表示出F点的坐标，表示出EF的长，进一步可表示出△CBE的面积，利用二次函数的性质可求得其取得最大值时E点的坐标.

考法三:二次函数的相似点问题

例3 (怀化)如图5，在平面直角坐标系中，已知抛物线y=ax²+bx-5与x轴交于A(-1,0),B(5,0)两点，与y轴交于点C.

(1)求抛物线的函数表达式.

(2)若点D是y轴上的一点，且以B,C,D为顶点的三角形与△ABC相似，求点D的坐标.

(3)如图6,CE∥x轴，与抛物线相交于点E,点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC,CE分别交于点F,G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积.

(4)若点K为抛物线的顶点，点M(4,m)是该抛物线上的一点，在X轴、y轴上分别找点P,Q，使四边形PQKM的周长最小，求出点P,Q的坐标.

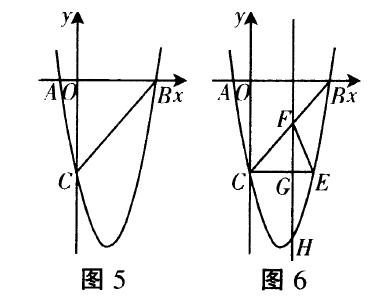
分析:(1)根据待定系数法直接求抛物线的函数表达式.(2)分两种情况，利用相似三角形的比例式即可求出点D的坐标.(3)先求出直线BC的解析式，进而求出四边形CHEF的面积的函数关系式，即可求出最大值.(4)利用对称性找出点P,Q的位置，进而求出P,Q的坐标.