中考中关于圆的五种相切的考法

切线的证明与计算题是全国中考的重要题型。切线的判定常在解答题中考查，切线的性质在选择题、填空题及解答题中均有考查，常结合三角形、四边形及二次函数相关知识。

1. 判定切线的方法：

（1）若切点明确，则“连半径，证垂直”。

常用方法：等角代换；全等证明；平行转化；有时可利用相似、勾股定理证垂直；

（2）若切点不明确，则“作垂直，证半径”。

常见手法：角平分线定理；等腰三角形三线合一，隐藏角平分线。

2. 典型基本图形：

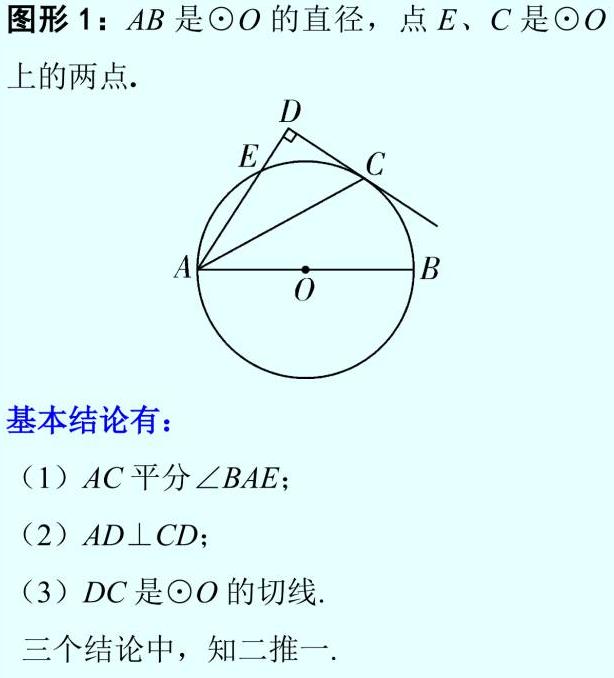
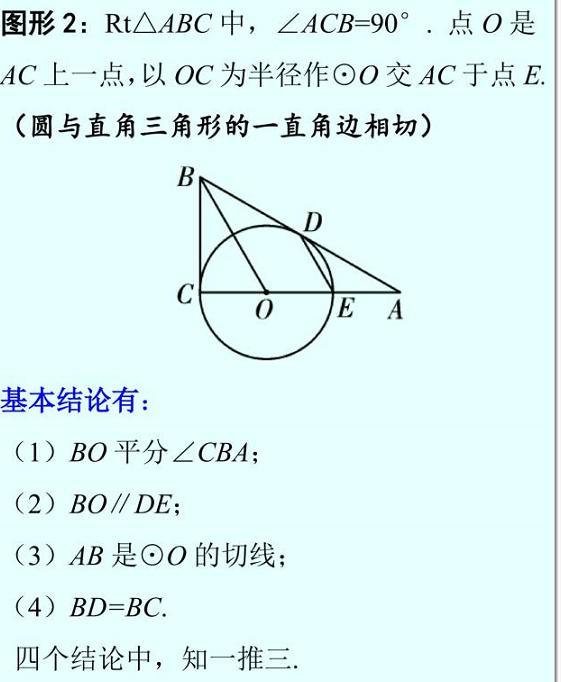
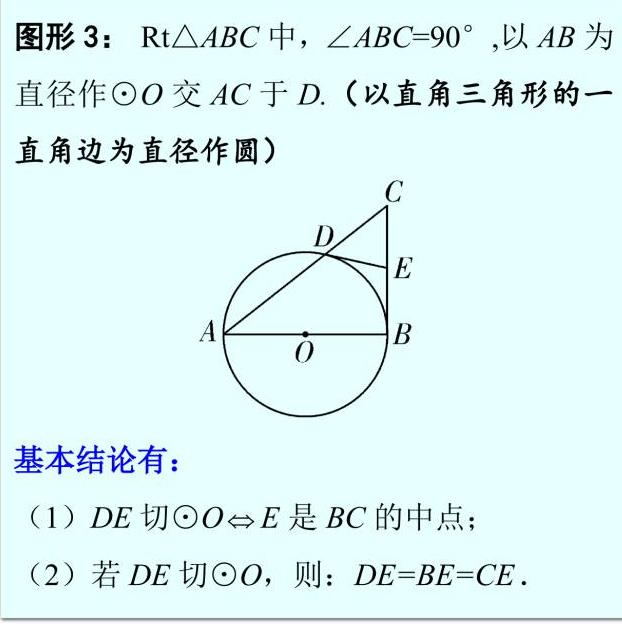
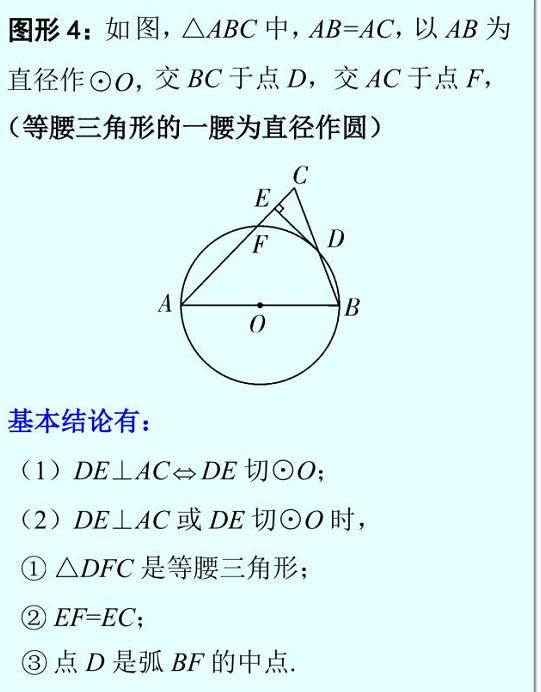
考点一：切线求角度和线段长

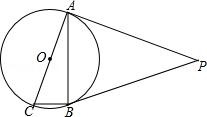
1．（2018•邻水县二模）如图，PA和PB是⊙O的切线，点A和B是切点，AC是⊙O的直径，已知∠P＝40°，则∠ACB的大小是（　　）

A．60° B．65° C．70° D．75°

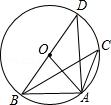
2．如图，△ABC内接于⊙O，∠BAC＝120°，AB＝AC＝4，BD为⊙O的直径，则BD等（　　）

A．4 B．6 C．8 D．12

考点二：切线与几何结合求线段长和半径

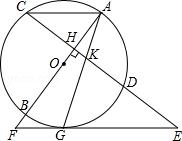
3.（2012•成都）如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F．切点为G，连接AG交CD于K．

（1）求证：KE＝GE；

（2）若KG2＝KD•GE，试判断AC与EF的位置关系，并说明理由；

（3）在（2）的条件下，若sinE＝3/5，AK＝2√5，求FG的长．