中考中常考的几何线段长的最值问题详细剖析

在中考中，最值问题属于“香饽饽”，属于每年必考题型。最值问题与动点问题并称初中最难的两个问题。常考的题型有两种，一是求线段的最小值，二是求面积的最大值。今天这篇文章就求线段的最小值进行详细剖析，希望能给大家带来帮助。

线段的最小值问题的理论依据就是:两点之间线段最短;直线外一点与直线上所有点的连线段中，垂线段最短;三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值).我们在解题时要学会转换努力向这三点靠拢，进而解决问题。

一、基本模型

1、轴对称模型

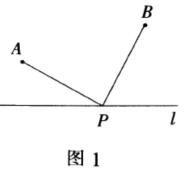
如图1 ：A,B为定点，L为定直线，P为直线L上的一个动点，求AP+BP的最小值.

2.折叠最值

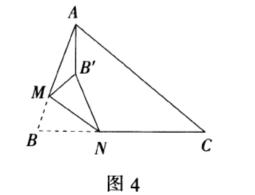
如图4，在△ABC中，M,N两点分别是边AB,BC上的动点，将△BMN沿MN翻折，

B点的对应点为B′，连结AB′，求AB′的最小值.

二、例题讲解

例1 : 如图5，点P是∠AOB内一定点，点M,N分别在边OA,OB上运动，若∠AOB=45°,OP=3√2，则△PMN的周长的最小值是多少？

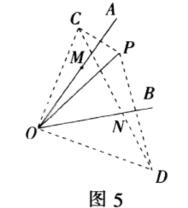
分析 作P关于OA,OB的对称点C,D.连结OC,OD，则当M,N是CD与OA,OB的交点时，△PMN的周长最短，最短的值是CD的长.根据对称的性质可以证得，△COD是等腰直角三角形，据此即可求解.

例2 ： 如图8,菱形ABCD中AB=2,∠A=120°，点P,Q,K分别为线段BC,CD,BD上的任意一点，则PK+QK的最小值是多少?

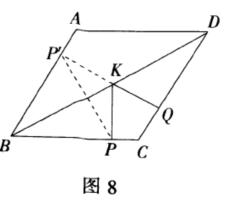
分析 根据轴对称确定最短路线问题，作点P关于BD的对称点P′，连结P′Q与BD的交点即为所求的点K.根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK+QK的最小值，然后求解即可.