数形结合思想：几何问题中运用代数法解题的三种基本类型

一、长度问题

例1 如图1，菱形ABCD的面积为120平方厘米时，正方形AECF的面积为50平方厘米，则菱形的边长为_________cm .

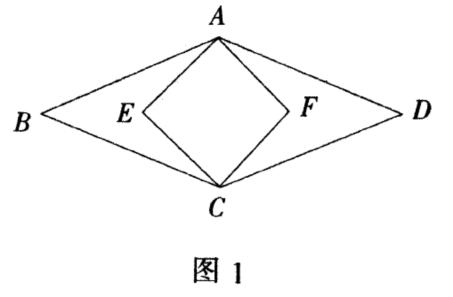
评析：本题的关键在于菱形和正方形都是轴对称图形且对角线都相互垂直的性质，通过数形结合的思想，设未知数，列出方程组解决问题。

二、面积问题

例2 如图，在△ABC中，∠BAC=45°,AD⊥BC,D为垂足,BD=6,CD=4，求△ABC的面积.

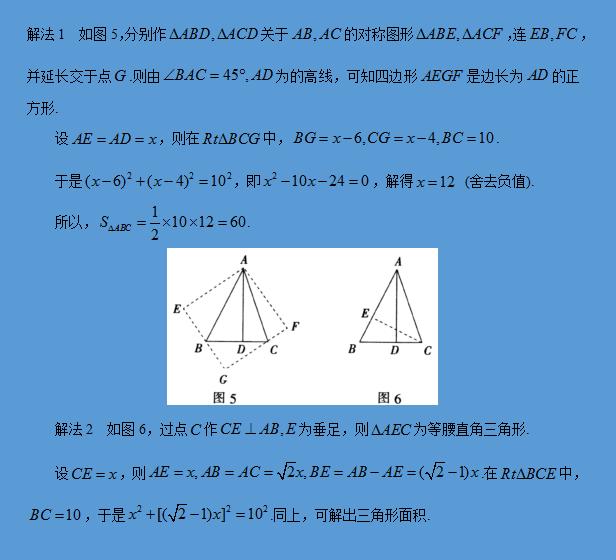
评析：本题关键在于通过直角三角形的性质，运用数形结合的思想设未知数，通过勾股定理列出方程求解，进而算出面积。

三、角度问题

例3 如图，正方形ABCD被两条与边平行的线段EF,GH分割成四个矩形，EF,GH交点为P.若矩形PFCH的面积恰为矩形PEAG的面积的两倍，试确定∠HAF的度数。

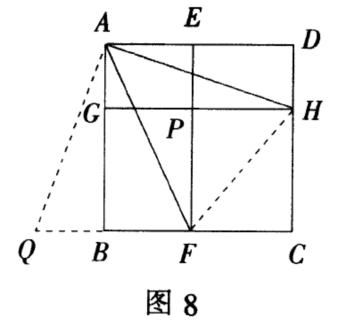
评析：本题的关键在于与正方形有关的角有90°,45°，观察图形，猜想∠HAF=45°.又正方形条件易实施旋转变换，由此可获求解途径.

最后送大家一首华罗庚教授关于数形结合的一首脍炙人口的诗:

数与形，本是相倚依，焉能分作两边飞.

数缺形时少直观，形少数时难人微.

数形结合百般好，隔裂分家万事休.

切莫忘，几何代数统一体，永远联系切莫离.