考点1 圆周角定理及其推论
1.定理:一条弧所对的圆周角等于它所对的圆心角的一半.
2.推论:(1)同弧或等弧所对的圆周角相等.
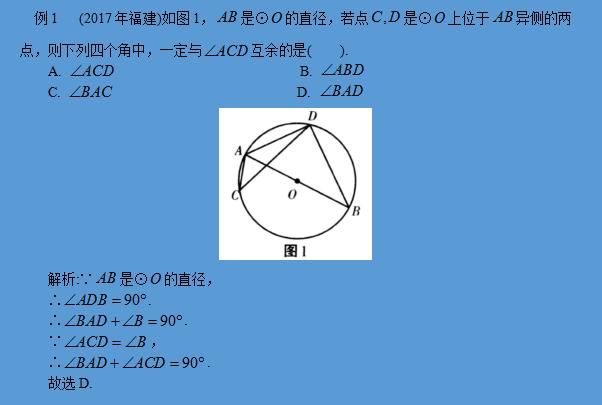
(2)半圆(或直径)所对的圆周角是直角,90º的圆周角所对的弦是直径.
考点2 弦、弧、圆心角、圆周角之间的关系
1.定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
2.推论:(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.
(2)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
温馨提示:1.在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对的其余两组量也相等.
2.一条弦(除直径外)所对应的弧有优弧、劣弧,优弧所对应的圆周角是钝角,劣弧所对应的圆周角是锐角,这一组圆周角互补一条弧只对着一个圆心角,却对着无数个圆周角.

考点3 垂径定理及其推论
1.定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
2.推论:(1)弦的垂直平分线经过圆心,并且平分弦所对的两条弧.
(2)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

考点4 圈内接四边形的性质
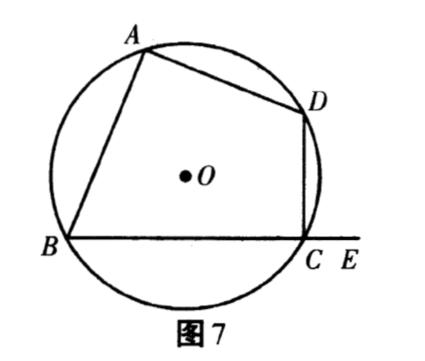
1.圆内接四边形的对角互补,如图7,∠A+∠BCD=180°,∠B+∠D=180°.
2.圆内接四边形的任意一个外角等于它的内对角,如图7,∠DCE=∠A.
考点5 点、直线与圆的位置关系
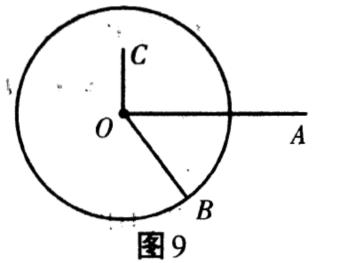
1.点与圆的位置关系:如图9,设圆的半径为r,平面内任一点到圆心的距离为d,则
(1)点在圆外→d>r,如点A;
(2)点在圆上→d=r,如点B;
(3)点在圆内→d<r,如点C.
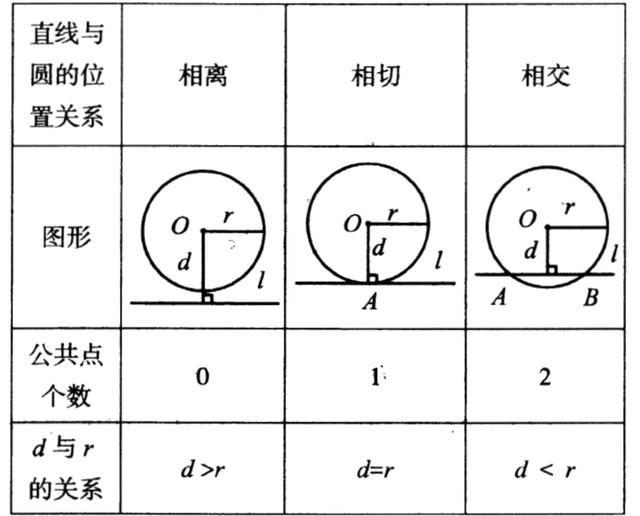
2.直线与圆的位置关系(r为圆的半径,d为圆心到直线的距离):

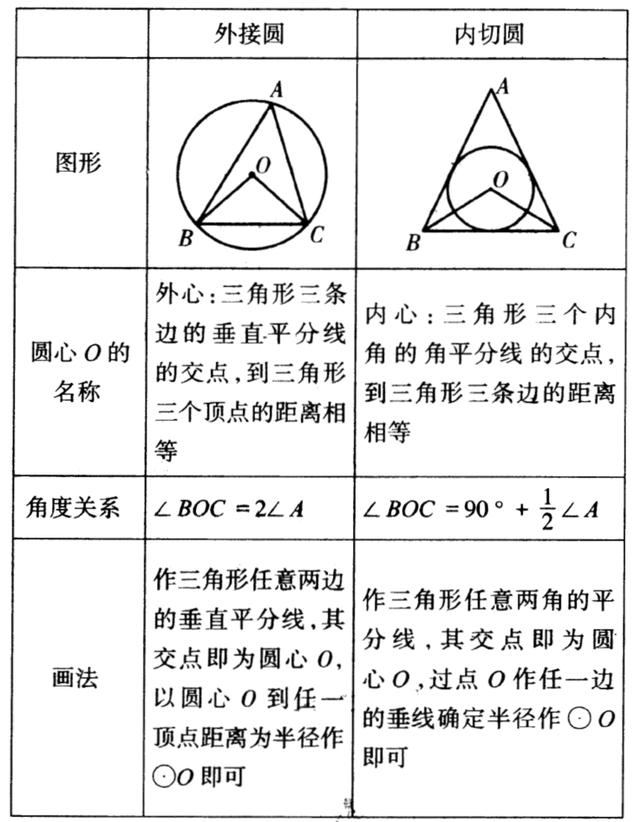
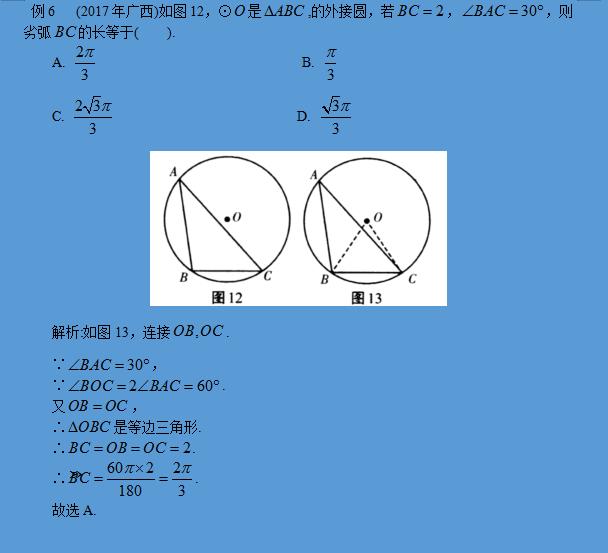
考点6 三角形的外接圆和内切图
考点7 正多边形与圆的关系
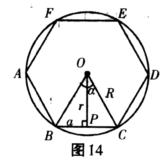
1.正多边形每一边所对的圆心角叫做正多边形的中心角.如图14,α为中心角,α=360°/n (n为正多边形的边数).
2.中心到正多边形的一边的距离叫做正多边形的边心距,如图14,OP为边心距.
3.r(边心距)、R(半径)、a(正多边形边长)的关系:r²+(a/2)²=R².

考点8 切线的性质及判定
1.切线的性质:圆的切线垂直于过切点的半径.
2.切线的判定:经过半径的外端并且垂直于这条半径的直线是圆的切线.
(1)当直线与圆的公共点已知时,连接圆心和公共点证明这条半径与直线垂直.
(2)当直线与圆的公共点未知时,过圆心向直线作垂线段,证明圆心到直线的距离等于半径.
(3)和圆只有一个公共点的直线是圆的切线.

考点9 弧长与扇形面积的有关计算
弧长l=nπr/180,扇形面积S=nπr²/360=1/2lr.其中r为圆的半径,n为弧所对的圆心角的度数,l是扇形的弧长.
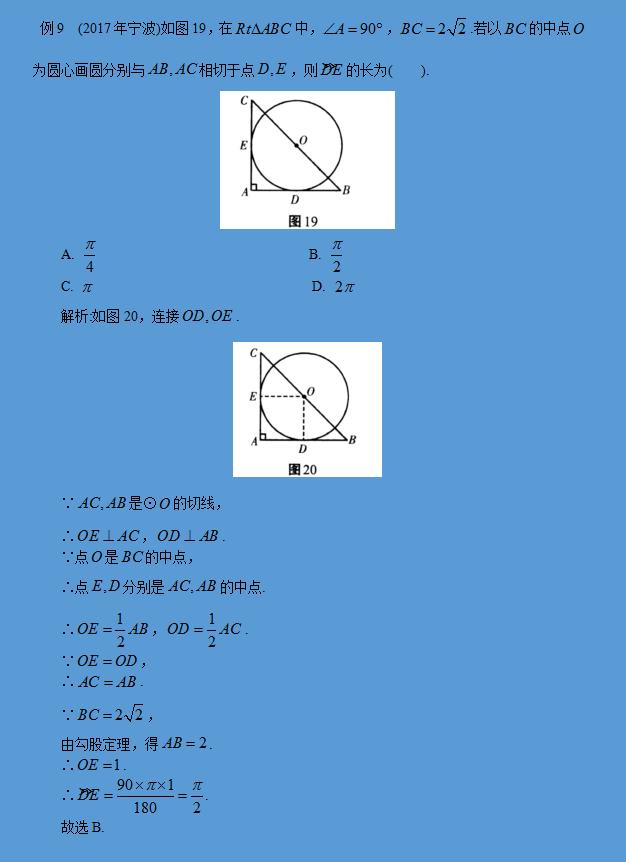
考点10 圆锥的有关计算
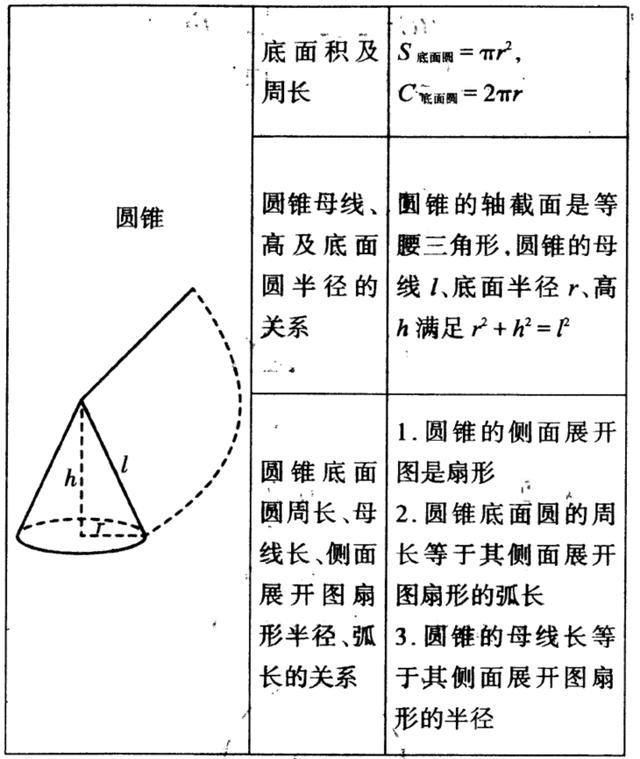
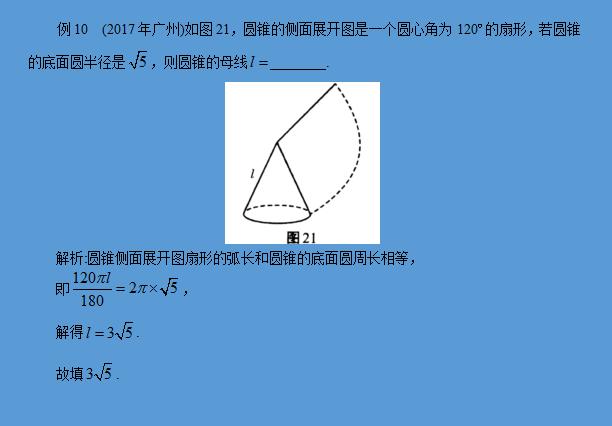
考点11 阴影部分面积的计算
1.规则图形:如扇形、圆、特殊四边形等,可直接利用面积计算公式计算.
2.不规则图形:通过“割补法”“平移法”“旋转法”等把不规则图形的面积转化为规则图形的面积.
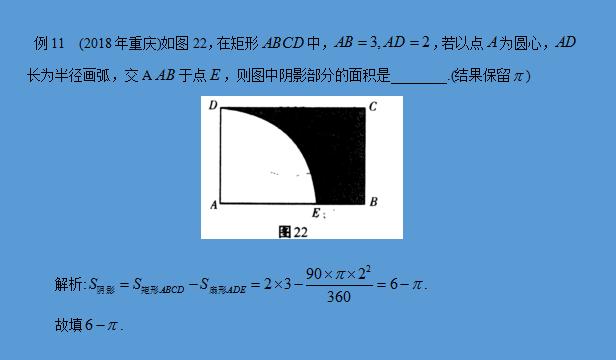

 加载中,请稍侯......
加载中,请稍侯......
精彩评论