在中考中五种常见的有关一次函数综合题考法

一、一次函数与反比例函数相结合

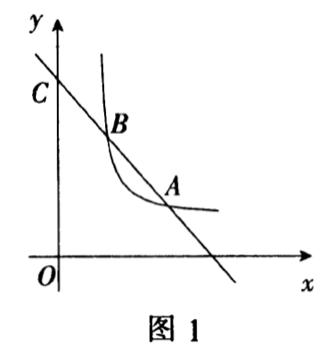
例1 如图1，函数y₁的图象与函数y₂=k₂/x(x＞0)的图象交于A,B两点，与y轴交于C点，已知A点坐标为(2,1),C点坐标为(0,3).

(1)求函数y₁的表达式和B点的坐标;

(2)观察图象，比较当x＞0时，y₁与y₂的大小.

二、一次函数与二次函数相结合

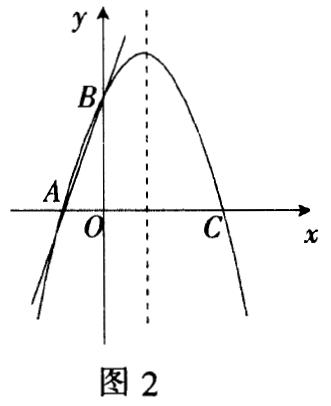
例2 如图2，直线y=3x+3交x轴于A点，交y轴于B点，过A,B两点的抛物线交x轴于另一点C(3,0).

(1)求抛物线的解析式;

(2)在抛物线的对称轴上是否存在点Q，使△ABQ是等腰三角形?若存在，求出符合条件的Q点坐标;若不存在，请说明理由.

三、一次函数与三角函数相结合

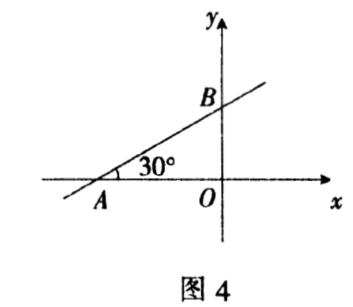
例3 如图4，直线y=kx+2与x轴的夹角为30°，与x、y轴的交点分别为A、B.

(1)求k的值;

(2)求不等式kx+2＜0的解集.

四、一次函数与直线相结合

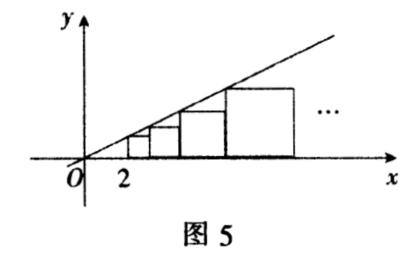
例4 如图5，在直线y=1/2x的下方依次作小正方形，每个小正方形的一个顶点都在直线

上，若左边最小的正方形左边顶点的横坐标是2，则从左到右第10个小正方形的边长是?

五、一次函数与圆相结合

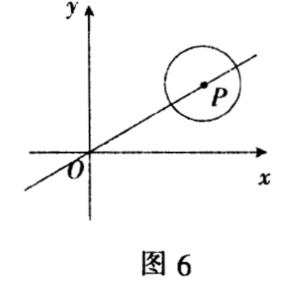
例5 如图6，在直角坐标系中，直线y=√3/3x上有一圆P，半径为1，圆心P的坐标为(2√3，m)，然后，让圆P沿直线向斜下方移动，速度为每秒1个单位，问经过多少秒后，圆P与x轴相切?