一道二次函数动点问题引发的思考，五种解法总有一种适合你

二次函数与动点相结合，属于初中阶段的难点题型，今天笔者就以一道二次函数动点问题为例剖析一下此类问题的几种解法。

例题：抛物线y=-1/3x+1/3x+4与x轴交于A,C两点，与y轴交于点B.在线段AC上取一点D使AD=AB.动点P从点A出发，以每秒1个单位长度的速度沿x轴向点C运动，运动时间为t秒.当点P关于直线BD的对称点在线段BC上时，t的值是_________.

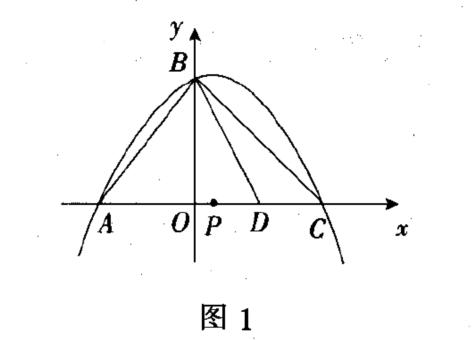
解法1：解析法

由解析式可以得出点A,B,C的坐标，根据AD=AB，得出D点坐标，以及直线BD的解析式.由于点P关于直线BD的对称点在线段BC上，那么点C关于直线BD的对称点就在直线BP上.如图2，由对称点连线被对称轴垂直平分，可以写出过点C及其对称点C＇的直线解析式.根据BC=BC＇，可得C＇点坐标，从而得出BC＇的解析式，求出点P的坐标.此法围绕轴对称性质，利用解析法，导向性强，能顺利解决问题.

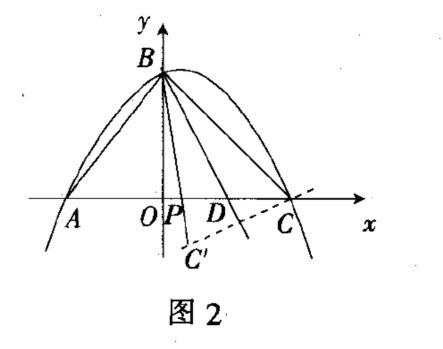
解法2：三角函数法

观察本题，易发现∠PBC=2∠DBC，掌握三角函数二倍角公式就很容易想到构造直角三角形，然后解直角三角形得出结论.（此处涉及到了二倍角公式属于高中知识，可拓展）

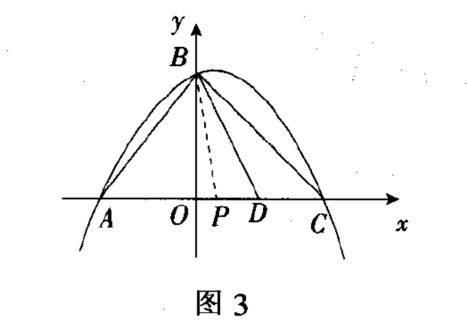
解法3：方程思想

类似解析法中思路，易得出图4.为求点P，可先求出C＇坐标.接着自然是借助向坐标轴作垂线段，构造直角三角形，再借助勾股定理列方程，使得问题得解.

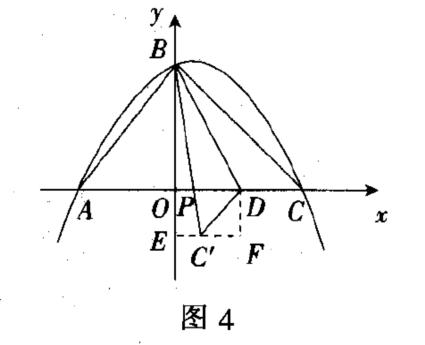
解法4：相似法

前三种方法思路较易形成，但计算量大.若平时能积累一些几何模型，本题借助构造相似三角形，可使得计算量大大减少.

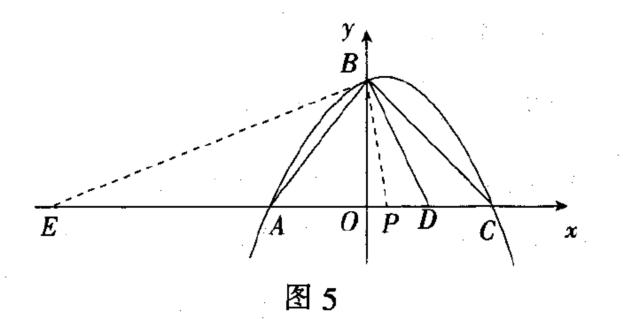
解法5：利用角平分线定理

本题利用角平分线定理，无需大量计算，也无需构造辅助线，推理过程大大缩短.

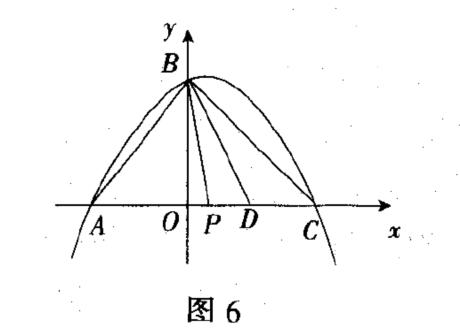
在以上五种解法中个人偏向于第四和第五种，方法计算量小，具有四两拨千斤之功效。