首先我们来看看韦达定理。

例1： f(x)= x² +（m-3)x+m=0 有两个根均大于0，求m的取值范围.

下面我们来看看运用零点存在性定理来解决二次函数零点问题求参数问题。

零点存在性定理：如果函数y=f(x)在区间[a,b]上的图像是连续不断的一条曲线，并且有f(a)f(b）＜0，那么，函数y=f(x)在区间（a,b)内有零点，即存在c∈（a,b)，使得f(c)=0，这个c也就是方程f(x)=0的根。

运用零点存在性定理求参，可分为两种题型：

题型一：

二次函数两个零点分别在两个区间。则只需这两个区间对应的两个端点函数值都异号即可。

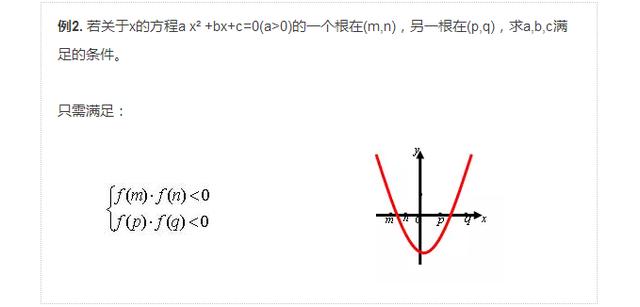
题型二：

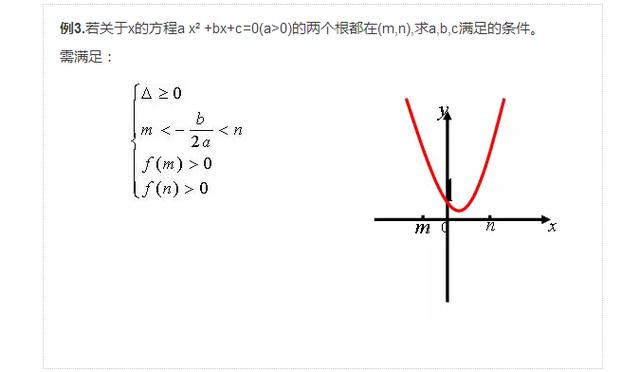
二次函数两个零点在同一个区间。此时需要：抛物线顶点在区间内；

‚抛物线顶点函数值与区间端点函数值异号，即可满足条件。

其中用对称轴在区间内去表征，‚用Δ、开口、区间端点正负去表征

同样对于例1：f(x)=x²+（m-3)x+m=0 有两个根均大于0，求m的取值范围。

表示两个根都在（0，+∞）上，其中+∞处端点值由开口决定，同理即可得：

以上便是根据二次函数零点求参数的方法，同学们学会了吗？

至于其他函数，一般也都是用零点存在性去求解，大家可以去试着举一反三哦。