高考常考静电场重难点汇总

一、电荷守恒、库仑定律的理解

1．两个完全相同的金属球接触后，所带正、负电荷先＂中和＂然后＂平均分配＂于两球。

分配前后正、负电荷之和不变。

2．当求两个导体球间的库仑力时，要考虑电荷的重新分布。

例：当两球都带正电时，电荷相互非斥而使电荷主要分布于两球的外侧,此时r将大于两球球心间的距离。

3．库仑定律是长程力，当r→0时，带电体不能看成质点，库仑定律不再适用。

4. 微观粒子间的库仑力远大于它们之间的万有引力，当计算微观粒子间的相互作用时可忽略粒子间的万有引力。

5. 计算库仑力时，先将电荷量的绝对值代入进行计算，然后根据电性来判断力的方向。

二、库仑力作用下的平衡问题

1. 解决平衡问题应注意三点

(1) 明确库仑定律的适用条件；

(2) 知道完全相同的带电小球接触时电荷量的分配规律；

(3) 进行受力分析，灵活应用平衡条件。

2.在同一直线上三个自由点电荷的平衡问题

(1) 条件：两个点电荷在第三个点电荷处的合场强为零，或每个点电荷受到的两个库仑力必须大小相等，方向相反。

(2) 规律

“三点共线”——三个点电荷分布在同一条直线上；

“两同夹异”——正、负电荷相互间隔；

“两大夹小”——中间电荷的电荷量最小；

“近小远大”——中间电荷靠近电荷量较小的电荷。

三、电场线的理解与应用

1. 两种等量点电荷的电场线

2. 分析带电粒子运动的轨迹类问题的技巧

四、静电力做功及电势差、电势能的计算方法

静电力做功与路径无关，只与初末位置有关。

计算方法：

⑴ 用功的定义式W=FScosθ来计算（F为恒力，仅适用于匀强电场中）。

⑵ 用“静电力做的功等于电势能的减少量”来计算

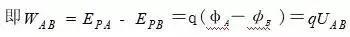
适用于任何电场．但WAB、UAB均有正负，要带符号进行运算。

⑶ 用由动能定理计算。

五、电场中电势、电势能高低的判定

1. 根据场源电荷判断（取无穷远为0势点）

离场源正电荷越近：电势越高（电势大于0），正检验电荷的电势能qφ越大，负检验电荷的电势能qφ越小。

离场源负电荷越近：电势越低（电势小于0），正检验电荷的电势能qφ越小，负检验电荷的电势能qφ越大。

2. 根据电场线判断电势、电场力做功判断电势能

顺着电场线的方向，电势一定依次降低，与放入场中的检验电荷的正、负无关．而电势能qφ则与q有关。

电场力对（正、负）电荷做正功，该电荷的电势能一定减少，由φ

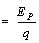
知当q为正时，电势φ亦减小，当q为负时，电势φ反而增加。

六、平行板电容器的动态分析

1. 确定不变量，分析是电压不变还是所带电荷量不变。

2. 根据决定式

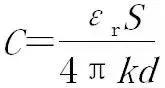
分析平行板电容器电容的变化。

3. 根据定义式

分析电容器所带电荷量或两极板间电压的变化。

4. 根据

分析电容器极板间场强的变化。

七、带电粒子(或带电体)在电场中的直线运动

1. 做直线运动的条件

(1) 粒子所受合外力F合＝0，粒子或静止，或做匀速直线运动。

(2) 粒子所受合外力F合≠0，且与初速度方向在同一条直线上，带电粒子将做匀加速直线运动或匀减速直线运动。

2. 用动力学观点分析

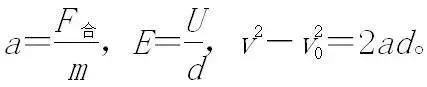
3. 用功能观点分析

匀强电场中：

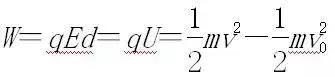
非匀强电场中：

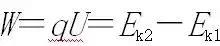
八、带电粒子在匀强电场中的偏转

1. 偏转问题

(1) 条件分析：带电粒子垂直于电场线方向进入匀强电场。

(2) 运动形式：类平抛运动。

(3) 处理方法：应用运动的合成与分解。

(4) 运动规律：

① 加速度：

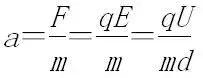
2. 两个结论

(1) 不同的带电粒子从静止开始经过同一电场加速后再从同一偏转电场射出时的偏转角度总是相同的。

(2) 粒子经电场偏转后，末速度的反向延长线与初速度延长线的交点O为粒子水平位移的中点，即O到电场边缘的距离为1/2。

3. 带电粒子在匀强电场中偏转的功能关系

当讨论带电粒子的末速度v时也可以从能量的角度进行求解：

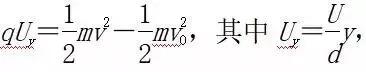
指初、末位置间的电势差。